Переконденсация пересыщенного пара: аналитические теории и численный эксперимент, страница 5

Для финитных функций (26) распределение капель локализовано в области размеров от  до , что не противоречит уравнению баланса вещества. Однако реализуется ли такое распределение динамически при любых параметрах начального финитного распределения? Чтобы проверить это и проследить за деталями процесса, мы, решая задачу численно,  вычисляли также и величину , строили графики функции  и следили за относительным расположением корней этого полинома и точки . 

Если  начальным ситуациям  соответствовали значения  (корней нет), то во всех рассмотренным нами случаях финальное автомодельное распределение возникало “бесконфликтно”  - величина  возрастала во времени, в определенный момент график  полинома  касался оси, но к этому моменту значение  оказывалось меньшим координаты точки касания, затем появлялись оба корня  и, которые постепенно занимали свои финальные положения, а величина   становилась все ближе и ближе к корню .

          Мы рассмотрели также экстремальную (видимо, не совсем реалистичную) ситуацию, когда  в  начальном состоянии  (т.е. корни   и  существуют), а значение  лежит между корнями. Результат расчета представлен на Рис.3 (второй график дает продолжение первого по времени).

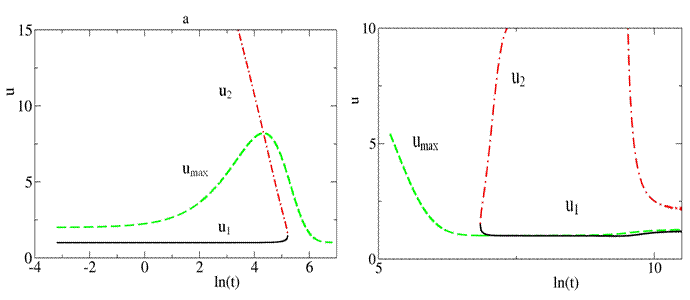Рис.3. Зависимость от времени минимального  u₁   и максимального u₂  корня полинома  и максимального размера капель u_max .

Из графиков видно, что и в этом случае автомодельное распределение реализуется. В начале процесса величина  убывает, а максимальный размер  растет, в некоторый момент его величина сравнивается с большим из корней, после чего   начинает убывать, причем его величина превосходит оба корня. В определенный момент величина   становится меньшей  27/4  и корни исчезают. На правой части Рис.3 показан момент, когда эти корни вновь возникают, к этому моменту значение  становится уже меньшим координаты точки касания оси графиком полинома , тем самым не происходит “запирания” части вещества в “опасной” зоне между корнями. В дальнейшем  принимает значение, очень близкое к значению минимального корня.

Для иллюстрации приведем для рассмотренного случая графики зависимости от времени функции распределения (Рис.4), а также критического радиуса и среднего размера капель (Рис.5).

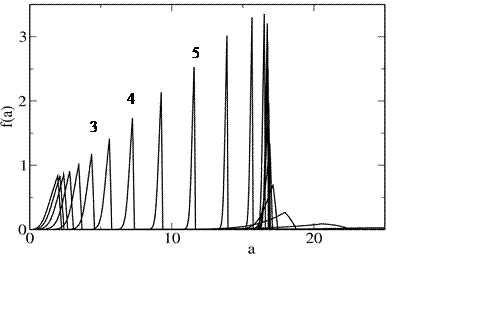
Рис.4. Функция распределения в разные моменты времени, начиная от , с шагом 0.5  по  (частные значения  указаны над пиками) .

Из Рис.4 видно, что функция распределения на начальном отрезке времени сужается и стремится занять некоторое предельное положение. Затем вступает в силу механизм переконденсации, который приводит к уширению функции и сдвигу максимума в область больших значений.

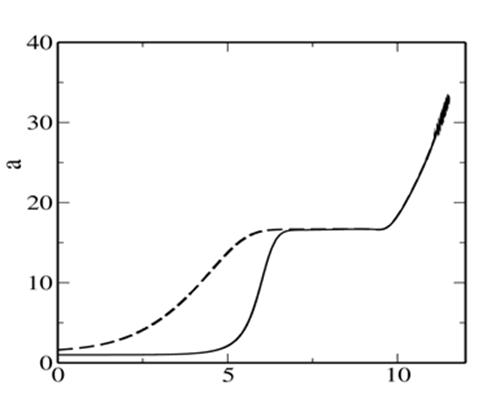Рис.5.Зависимость от времени среднего размера капель и критического размера.

На Рис.5 показано изменение во времени среднего размера капель и критического размера. На первой стадии процесса, когда общая масса капель нарастает за счет потребления избыточного пара, рост среднего размера капель  опережает относительно медленное возрастает критического размера. По мере падения пересыщения  ситуация меняется – рост  замедляется, а большая разность между  и  приводит к быстрому росту критического радиуса, который практически сравнивается со средним размером капель. Подчеркнем, что это происходит намного раньше, чем устанавливается окончательное автомодельное распределение. В дальнейшем на довольно значительном промежутке времени  и  остаются практически постоянными. Это соответствует начальному этапу переконденсации, на котором функция распределения уширяется (крупные капли растут за счет маленьких), но его левый край еще не достиг нулевого размера и общее число капель практически остается неизменным. Затем наступает этап быстрого убывания общего числа капель, который сопровождается ростом среднего радиуса капель и критического радиуса (они остаются при этом практически равными друг другу), этот этап завершается в конечном счете установлением финального автомодельного распределения. Проиллюстрируем также сказанное графиком зависимости от времени номера исчезающей капли на Рис.6.