Переконденсация пересыщенного пара: аналитические теории и численный эксперимент, страница 3

                           (23)

Таким образом, уравнение (21), определяющая конкретный вид автомодельного решения (8), (10), содержит произвольный  параметр . Встает вопрос о  возможных физических значениях этого параметра, из его определения (22) очевидно пока только, что  .

При  и любых  решение уравнения (21) имеет асимптотику , при  и любых  асимптотика имеет вид . Такой вид асимптотики при малых  согласуется с (7), обеспечивая конечность скорости убыли числа капель (6), асимптотика при больших  означает, что в качестве решения можно выбирать лишь финитные функции – такие, что  при , в противном случае не будет существовать интеграл в уравнении баланса вещества (4) .

Область допустимых значений параметра  определяется полиномом

,                                    (24)

стоящим множителем при производной в уравнении (21). Чтобы финитное решение этого уравнения было корректным, необходимо, чтобы выполнялось условие

                                        (25)

в случае если , и обращения в нуль также и полинома в правой части (21) в случае . Полином  при любых  имеет как минимум один вещественный корень. Учитывая, что , видно, что локальный минимум  находится в точке , а локальный максимум  – в точке . Отсюда заключаем, что этот всегда присутствующий корень отрицателен  .  На роль же , согласно (25), может претендовать положительный корень полинома .

На Рис.1 показаны графики  в области локализации положительных корней .

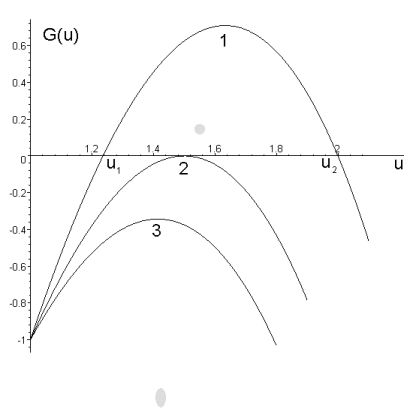 Рис.1. График функции  при различных значениях параметра   :    для кривой 3,     для кривой 2,      для кривой 1.

Такие корни существуют при , при  они сливаются в один корень . Отметим, что для полинома (24) сумма корней равна нулю: .

Таким образом, допустимые значения параметра   лежат в области . Зная корни полинома (24), нетрудно проинтегрировать уравнение (21). Результат можно представить в виде

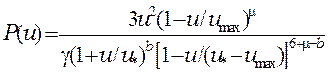,                         (26)

где .   В качестве независимого параметра в решении (26) выбран показатель , прочие параметры, в том числе исходный независимый параметр , выражаются через  соотношениями

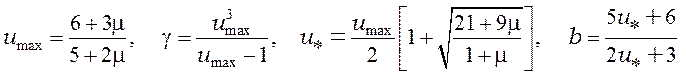.   (27)

Для решений, удовлетворяющих условию  , параметр  может лежать в диапазоне , этому соответствуют значения максимального радиуса капель в диапазоне , параметр же  монотонно убывает от  при  до  при . Случай , при котором   (обрыв на правом краю распределения),  также допустим, так как при этом полином в правой части (21) обращается в ноль в точке .

Таким образом, область физических значений параметра  лежит в диапазоне , которому соответствует диапазон  параметра . Аккуратное рассмотрение предельного случая  показывает, что при этом (26) переходит в функцию Лифшица-Слезова (9), если учесть, что в этом случае , что приводит к появлению в (26) множителя вида  , дающего в пределе .

На Рис.2 изображены графики функции (26)  при различных значениях параметра .

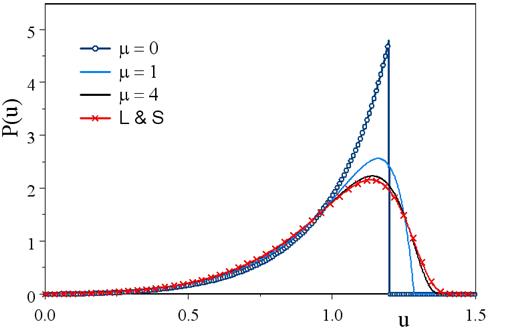
Рис.2.  Функция  для трех  значений параметра  и функция Лифшица-Слезова.

Приведем некоторые общие свойства автомодельного распределения  (26). Проинтегрируем обе части уравнения (21) в пределах от  до. Интегрируя в левой части уравнения по частям и учитывая (25), получим

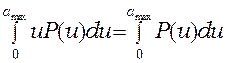,                                     (28)

откуда следует, что .  Это соотношение означает равенство критического и среднего радиуса капель в автомодельном распределении при любых допустимых значениях параметра . Интеграл в правой части (28) на самом деле равен единице при выбранной нормировке функции  в (26). Чтобы это доказать, надо повторить  описанную процедуру интегрирования уравнения (21), разделив предварительно на  обе его части, это приводит к соотношению

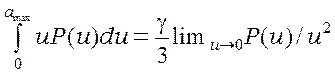.                       (29)

Из  (26) видно, что правая часть этого соотношения равна единице, с учетом (28) это показывает, что функция (26) действительно нормирована на единицу.

Приведем результаты для основных физических величин в исходных обозначениях. Для критического радиуса из (23), (14) и (15) находим

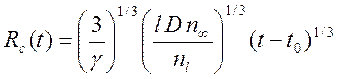.                     (30)

Для числа капель в единице объема из (5), (8), (26) имеем

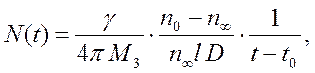                           (31)