Переконденсация пересыщенного пара: аналитические теории и численный эксперимент, страница 2

Действительно, как показано в работах  [4-6], функция (9) не является единственной, делающей автомодельное представление (8), (10) решением уравнения (3). Она соответствует начальным функциям , достаточно хорошо убывающим при больших , но для которых отсутствует понятие максимальной капли. Для “финитных” начальных распределений  (существует максимальная капля), возможны другие варианты автомодельного решения  (8), (10) (с другими функциями ). В настоящей работе путем численного решения уравнений (2)-(4) мы хотели проверить, действительно ли всегда реализуется один из вариантов асимптотического решения (8), (10) и выяснить, почему для финитных распределений  оказываются недействительными аргументы Лифшица-Слезова в пользу выбора универсального решения (9).

 ВЫЧИСЛИТЕЛЬНАЯ ПРОЦЕДУРА

Для реализации процедуры численного решения уравнения (2)–(4) были преобразованы к более удобному виду, не содержащему размерных параметров, путем введения безразмерных переменных

,   (14)

где – величина критического радиуса в начальный момент времени,

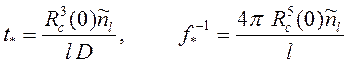 .                     (15)

Вторая модификация затрагивает уравнение баланса вещества (4). Сложность его использования состоит в том, что для нахождения из (4) очень малой величины пересыщения пара  на фоне прочих входящих в это уравнение больших величин требуется очень высокая точность вычисления последних (поскольку они почти точно компенсируются). Мы сочли более удобной другую форму уравнения баланса вещества, которая получается из (4) дифференцированием по времени и использованием уравнений (2), (3). Принимая в качестве независимой переменной критический радиус и исключая  с помощью (1), можно записать получающееся уравнение в  безразмерных переменных (14) в виде                                                                                           

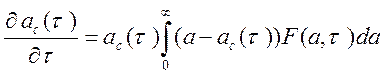.                 16)

В этом уравнении мы перешли затем к представлению Лагранжа

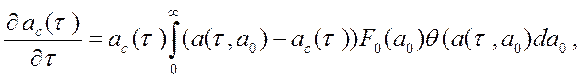         (17)

заменив усреднение с функцией распределения в момент времени  на усреднение с начальной функцией распределения и перебросив зависимость от времени на траектории “представляющих точек”   – решения уравнения

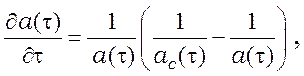                          (18)

с начальным условием .  В некоторый момент времени величина  может оказаться равной нулю, а затем перейти в отрицательную область, соответствующие вклады в среднее значение в (17) необходимо отбросить, поэтому в подынтегральное выражение введена

В качестве  выбирались функции, локализованные в области  Эта область разбивалась на 10000 частей  Каждая из точек разбиения служила начальным условием для траектории, совокупность которых находилась из решения уравнений (17), (18). Для ускорения расчетов временной шаг постепенно увеличивался со временем. Нами использовался также  другой способ расчета – выбирались только 2000 представляющих точек, но через некоторое  время исчезнувшие к этому моменту точки восстанавливались с помощью квадратичной интерполяции. Результаты расчетов обоими методами совпадают. Однако второй способ вычислений работает значительно быстрее и позволяет продвинуться дальше по времени.

По найденным траекториям  функция распределения в момент времени   находилась с использованием соотношения

 ,          (19)   где  – интервал, в который перешел интервал  при движении его концов по траекториям. Правая часть (19) представляет собой число капель в интервале  в начальный момент времени, левая – равное ему число капель в момент . Из (19) находим

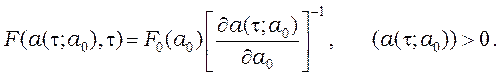             (20)

При приближенном вычислении производная в (20) заменялась на отношение соответствующих конечных интервалов.

 ОБЩИЙ ВИД АВТОМОДЕЛЬНОГО РЕШЕНИЯ

Прежде чем переходить к изложению результатов, полученных  численным интегрированием уравнений, рассмотрим общий вид автомодельного решения. Подставляя автомодельный анзац (8) в уравнение (3), получаем

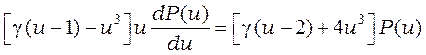,              (21)

где

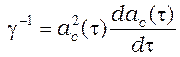 .                                        (22)

Чтобы решение уравнения (21), как это предполагалось, не зависело от , необходимо, чтобы не зависел от  определенный соотношением (22) параметр . Этому, в согласие с (10), отвечает степенная зависимость критического радиуса от времени