где ![]() -
третий момент функции
-
третий момент функции ![]() (26). Как уже отмечалось, средний
размер капель
(26). Как уже отмечалось, средний
размер капель ![]() имеет то же асимптотическое
выражение, что и критический размер
имеет то же асимптотическое
выражение, что и критический размер ![]() , т.е. описывается
соотношением (30) . Уравнение (16) позволяет найти малое отличие этих величин.
В размерных переменных это уравнение, с учетом (14), (15), может быть
переписано в виде
, т.е. описывается
соотношением (30) . Уравнение (16) позволяет найти малое отличие этих величин.
В размерных переменных это уравнение, с учетом (14), (15), может быть
переписано в виде
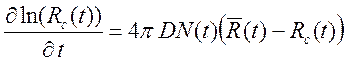 , (32)
, (32)
откуда, используя (30), (31), находим
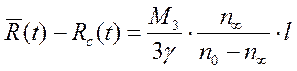 . (33)
. (33)
Амплитуды в асимптотических
выражениях (30), (31) и (33) плавно зависят от параметра ![]() автомодельного распределения (8), (26). Величина
автомодельного распределения (8), (26). Величина
![]() в (30) монотонно возрастает от значения
0,703 при
в (30) монотонно возрастает от значения
0,703 при ![]() до 0.763 при
до 0.763 при ![]() , а
величина
, а
величина ![]() в (31) и (33) монотонно возрастает в этой
области от 0,127 до 0,167. Отметим, что соотношение (33) показывает, что
разность между величиной среднего радиуса капли и критическим радиусом
в (31) и (33) монотонно возрастает в этой
области от 0,127 до 0,167. Отметим, что соотношение (33) показывает, что
разность между величиной среднего радиуса капли и критическим радиусом ![]() , т.е. на несколько порядков меньше, чем
каждый из них. Тем не менее, именно эта величина является “движущей силой”, определяющей
эволюцию критического размера. Это показывает, что при численном решении
уравнения (32) (точнее, его безразмерного аналога (16)) необходимо выдерживать
достаточно высокую точность вычислений.
, т.е. на несколько порядков меньше, чем
каждый из них. Тем не менее, именно эта величина является “движущей силой”, определяющей
эволюцию критического размера. Это показывает, что при численном решении
уравнения (32) (точнее, его безразмерного аналога (16)) необходимо выдерживать
достаточно высокую точность вычислений.
ЗАВИСИМОСТЬ АВТОМОДЕЛЬНОГО РЕШЕНИЯ ОТ НАЧАЛЬНОЙ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ
Численный расчет показывает,
что в зависимости от вида начальной функции распределения на больших временах
реализуется одна из автомодельных функций (26) с некоторым значением параметра ![]() . Как показано в [4,5], это значение
целиком определяется поведением начальной функции
. Как показано в [4,5], это значение
целиком определяется поведением начальной функции ![]() в
окрестности максимальной капли. Это связано с тем, что имеет место следующий
“закон сохранения” : если начальная функция распределения
в
окрестности максимальной капли. Это связано с тем, что имеет место следующий
“закон сохранения” : если начальная функция распределения ![]() имела в окрестности максимального размера
вид
имела в окрестности максимального размера
вид
![]() (34)
(34)
то он сохраняется и во все последующие моменты времени:
![]() (35)
(35)
Это означает, что такое же поведение
в окрестности максимальной капли должна иметь автомодельная функция
распределения, что позволяет отождествить показатель ![]() в
(26) с показателем в начальном распределении (34).
в
(26) с показателем в начальном распределении (34).
Поясним происхождение соотношения (35). Подставляя в (20) асимптотику (34), получаем
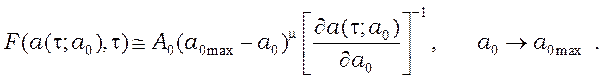 (36)
(36)
Производную в (36) можно заменить ее значением в точке ![]() . Существенно, что величина
. Существенно, что величина 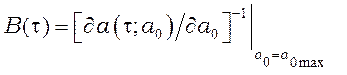 не обращается в нуль ни при каких значениях
времени
не обращается в нуль ни при каких значениях
времени ![]() . Рассмотрим точку
. Рассмотрим точку ![]() ,
близкую к точке
,
близкую к точке ![]() , и выберем в (36) точку
, и выберем в (36) точку ![]() так, чтобы
так, чтобы ![]() . Из
(36) тогда получим
. Из
(36) тогда получим
![]() . (37)
. (37)
В момент времени ![]() точка
точка ![]() в (33)
перейдет в точку
в (33)
перейдет в точку ![]() , а точка
, а точка ![]() - в точку
- в точку![]() .
Пользуясь малостью соответствующих интервалов, можно записать
.
Пользуясь малостью соответствующих интервалов, можно записать ![]() Подставляя это выражение в (37), приходим
к соотношению (35) с
Подставляя это выражение в (37), приходим
к соотношению (35) с ![]()
АРГУМЕНТЫ ЛИФШИЦА-СЛЕЗОВА О ВЫБОРЕ
ПАРАМЕТРА ![]()
Представляет интерес
рассмотреть, почему для финитных спектров не срабатывают аргументы
Лифшица-Слезова о выборе значения параметра ![]() .
Переписывая, следуя [1-3], уравнение движения (18) в терминах переменной
.
Переписывая, следуя [1-3], уравнение движения (18) в терминах переменной ![]() , получим
, получим
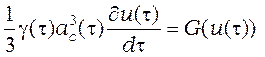 ,
,
![]() , (38)
, (38)
где ![]() -
полином (24) с
-
полином (24) с ![]() из (22). Множители при производной
в правой части (38) положительны, поэтому знак производной определяется знаком
полинома в правой части уравнения. В асимптотическом автомодельном режиме (8),
(10) величина
из (22). Множители при производной
в правой части (38) положительны, поэтому знак производной определяется знаком
полинома в правой части уравнения. В асимптотическом автомодельном режиме (8),
(10) величина ![]() принимает некоторое постоянное
значение. В зависимости от этого значения имеется три варианта расположения
графика полинома
принимает некоторое постоянное
значение. В зависимости от этого значения имеется три варианта расположения
графика полинома ![]() , которые показаны на Рис.1. В
[1-3] аргументируется, что только второй из них (касание оси абсцисс)
согласуется с законом сохранения вещества для систем, в которых отсутствует
понятие максимальной капли. Действительно, если бы финальное состояние соответствовало
кривой 3, то капли с размерами, большими
, которые показаны на Рис.1. В
[1-3] аргументируется, что только второй из них (касание оси абсцисс)
согласуется с законом сохранения вещества для систем, в которых отсутствует
понятие максимальной капли. Действительно, если бы финальное состояние соответствовало
кривой 3, то капли с размерами, большими ![]() (таковые,
хотя бы в небольшой количестве, всегда присутствуют в системе с неограниченным
спектром размеров), имея отрицательную производную в (38), скопились бы в точке
(таковые,
хотя бы в небольшой количестве, всегда присутствуют в системе с неограниченным
спектром размеров), имея отрицательную производную в (38), скопились бы в точке
![]() . К ним добавились бы и капли из промежутка
между корнями. Однако в автомодельном режиме фиксированной точке
. К ним добавились бы и капли из промежутка
между корнями. Однако в автомодельном режиме фиксированной точке ![]() соответствует, в силу (23), (38),
неограниченно растущий размер капли
соответствует, в силу (23), (38),
неограниченно растущий размер капли ![]() , что противоречит
закону сохранения вещества. Этот закон будет нарушен и в случае финального
состояния, описываемого кривой 1, поскольку в нем все капли имеют отрицательную
производную в (38).
, что противоречит
закону сохранения вещества. Этот закон будет нарушен и в случае финального
состояния, описываемого кривой 1, поскольку в нем все капли имеют отрицательную
производную в (38).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.