Числовое программное управление, автоматизированное проектирование и изготовление с помощью ЭВМ (Глава 5 книги "Роботы и автоматизация производства"), страница 4

Двоично-десятичный код. Двоично-десятичный код используется для записи информации не только на перфолентах, но и на магнитных лентах, а также в запоминающих устройствах с произвольной выборкой. Обычно инженеру по автоматизации нет необходимости читать двоично-десятичный код без помощи считывающего устройства, однако стоит научиться читать этот код, так же как и понимать структуру числового кода, используемого на  станках с  ЧПУ. При ближайшем рассмотрении рис. 5.6 можно заметить, что на перфоленте шириной 1 дюйм (25,4 мм) имеется восемь равномерно расположенных «дорожек» (рядов отверстий по длине ленты) плюс еще одна дорожка отверстий поменьше ближе к середине. Малые отверстия предназначены для ведущей звездочки механизма, перемещающего ленту при набивании или считывание программы. Обратите внимание, что эта дорожка, называемая транспортной, расположена между третьей и четвертой дорожкой, а не посередине ленты между четвертой и пятой. Это было сделано специально и очень разумно, поскольку исключает возможность неправильной установки ленты на станке и неправильного визуального считывания. На рис. 5.7 приведена расшифровка двух двоично-десятичных кодов, применяемых на станках с ЧПУ. Каждая цифра здесь представлена сочетанием отверстий из восьми возможных в горизонтальном ряду. Информация на перфоленте чаще всего записывается с помощью традиционного кода EIA244А Ассоциации электронной промышленности, показанного на рис. 5.7 справа.

Рис. 5.6

Перфолента (а) и перфокарта (б)

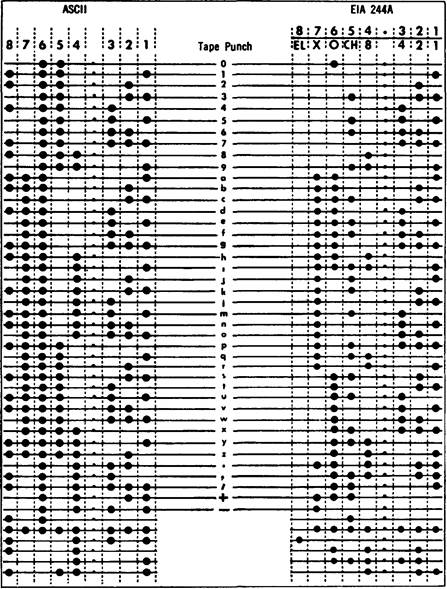
Рис. 5.7

Сравнение двух двоично-десятичных кодов, применяемых для программного управления

Для записи всех десятичных цифр используются четыре двоичных знака. Эти знаки занимают на перфоленте дорожки с первой по четвертую, как это указано в табл. 5.1. В двоично-десятичной системе счисления четыре двоичных знака требуются для изображения одной десятичной цифры, чтобы облегчить ее восприятие, хотя бы и за счет несколько большего количества знаков двоичного числа. В табл. 5.2 приведены для сравнения десятичные цифры и их написание в двоично-десятичной и двоичной системах счисления. Обратите внимание, что написание десятичных цифр от 0 до 9 включительно в двоичном и двоично-десятичном счислениях совпадают. При написании десятичного числа 10 в двоично-десятичном коде добавляется еще один двоичный знак (как и в десятичном), и оно начинает считаться снова, начиная с нижнего порядка. Чисто двоичные числа продолжают иметь четыре знака, пока все возможные комбинации не будут исчерпаны. Таким образом, двоичная система более эффективна, но труднее для прочтения. Если читатель усвоил описываемый метод, он уже может написать двоично-десятичный эквивалент любого десятичного числа, а чисто двоичный — нет. Попробуйте проделать это для десятичного числа 1439. Написание числа в двоично-десятичной системе проиллюстрировано на рис. 5.8.

5.1. Привязка дорожек перфоленты к десятичным числам *

* Например, для представления десятичного числа 9 на дорожках с первой по четвертую будет пробито двоичное число: 1001.

5.2. Соотношение между числами в десятичной, двоично-десятичной и двоичной системах счисления