Силовой анализ механизмов. Определение сил, действующих на механизм.

4. Силовой анализ механизмов.

На каждое звено механизма действуют силы (моменты) со стороны других звеньев, образующих с ними кинематические пары. Эти силы приложены к элементам кинематических пар и в дальнейшем реакциями в кинематических парах. На звенья механизма могут действовать также силы (моменты) со стороны других объектов, участвующих в работе механизма. Эти силы называются действующими или приложенными.

При силовом анализе механизма действующие силы должны быть известны, а подлежат определению уравновешивающий момент и реакции во всех кинематических парах. Решение этих задач основано на применении принципа Даламбера, согласно которому звено механизма можно рассматривать как находящиеся в равновесии, если ко всем внешним силам, действующим на него, добавить силу инерции.

Силовой анализ механизмов проводиться для того, чтобы в последствии по найденным силам (моментам) произвести расчет на прочность элементов кинематических пар и звеньев механизма, а также правильно подобрать привод.

При силовом исследовании обычно, по крайней мере, на первом этапе силами трения в кинематических парах пренебрегают, так как они часто невелики по сравнению с другими силами, действующими на механизм.

Силовой анализ механизма проводят как аналитическими, так и графическими методами в соответствии со следующим алгоритмом:

1. определяют силы инерции звеньев;

2. выделяют структурные группы Ассура;

3. начиная с последней структурной группы, в которую входит выходное звено, последовательно определяют реакции во всех кинематических парах;

4. из условий равновесия начального звена находят уравновешивающий момент и реакцию, действующую на него со стороны стойки.

Силовой анализ механизмов в курсовом проекте выполняется обоими методами только для исследуемого (то есть для второго (j₁ = 165°)) положения.

4.1. Определение сил, действующих на механизм.

4.1.1. Определение сил инерции.

При движении звена различные его точки в общем случае имеют различные ускорения. По принципу Даламбера к каждой точке звена, обладающей элементарной массой dm, следует приложить элементарную силу инерции , где а – ускорение массы dm. Так как звено имеет множество точек, то и сил инерции, действующих на звено, – множество. На практике при расчете самого звена на прочность ограничиваются конечным числом сил инерции, которые сосредотачивают в центрах тяжести. В дальнейшем обычно эти силы приводят к центру масс S звена. В результате на центр масс звена действует результирующая сила инерции (главный вектор инерции), называемая силой инерции F_И, и главный момент сил инерции звена (момент пары сил инерции) М_И. Сила инерции F_И и момент пары сил инерции М_И определяются по формулам соответственно:

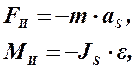
где m – масса звена; а_S – вектор ускорения центра масс; J_S – момент инерции звена относительно оси, проходящей через центр масс перпендикулярно плоскости движения; e – угловое ускорение звена. Знак минус показывает, что сила и момент инерции направлены противоположно ускорению.

Находим для исследуемого станка угловые ускорения звеньев и линейные ускорения центров масс звеньев в проекциях на оси координат.

Для начального звена во втором положении (см. 3.5) соответственно будем иметь

Для остальных звеньев ускорения центров масс и угловые ускорения находим по формулам, связывающими их с аналогами скоростей и ускорений [2,3], которые имеют следующий вид:

;    ;    .             (4.1)

Результаты расчета ускорений звеньев механизма по формулам (4.1) приведены в табл. 4.1.

Таблица 4.1.

Ускорения центров масс и угловые ускорения звеньев.

Определив ускорения звеньев, находим главный вектор и главный момент сил инерции звеньев механизма. Тогда соответственно главный вектор сил инерции и главный инерционный момент звеньев механизма определится:

Для звена 1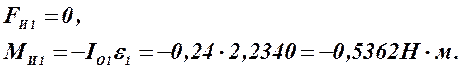          

Для звена 3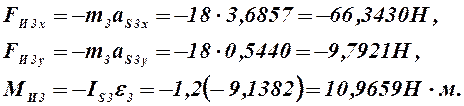          

Для звена 4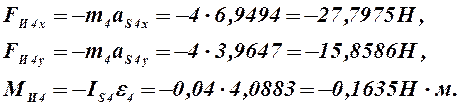          

Для звена 5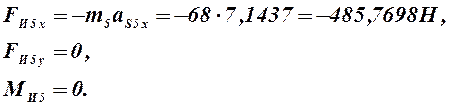          

4.1.2. Силы, действующие на механизм.

Для удобства дальнейшей работы в табл. 4.2 сведены все действующие на механизм силы и моменты в проекциях на оси координат со своими знаками.

Таблица 4.2

Силы и моменты, действующие на механизм.

Сила резания	Сила веса, Н			Силы инерции, Н					Моменты сил инерции, Н×м
Fcx, H	F3y	F4y	F5y	FИ3x	FИ3y	FИ4x	FИ4y	FИ5x	МИ1	МИ3	МИ4
-2000	-176,5800	-39,2400	-667,0800	-66,3430	-9,7921	-27,7975	-15,8586	-485,7698	-0,5362	10,9659	-0,1635

Так как направления сил и моментов учтены их знаками, то на расчетных схемах все силы изображаем в направлении координатных осей, а моменты – против хода часовой стрелки.

4.1.3. Реакции, действующие в кинематических парах.

Реакция (сила) считается определенной, если известны ее точка приложения, величина (модуль) и направление. Для наиболее распространенных на практике кинематических цепей, которые существуют в трехподвижном пространстве (П = 3), допускающем два независимых поступательных перемещения вдоль осей Х и Y и одно вращательное вокруг оси Z, число неизвестных, однозначно определяющих реакцию в кинематической паре, не превышает двух.

Так для вращательной пары неизвестными являются модуль реакции F_ij, действующей i–ое звено со стороны j–ого звена, и направление, характеризуемое углом a, известна точка приложения. Для поступательной пары неизвестны модуль F_ij и координата х, а известно направление (реакция направлена по нормали к траектории движения). Высшая контактная кинематическая пара имеет одну неизвестную – модуль F_ij, а известны у нее направление (нормаль к соприкасающимся поверхностям) и точка приложения (место контакта).