4.2. Определение уравновешивающего момента и реакций в кинематических парах аналитическим методом.
Силовой анализ механизма аналитическим методом проводится последовательно и отдельно для каждой структурной группы, начиная с той, в которую входит выходное звено. Начальное звено анализируется последним.
Для определения реакций в кинематических парах структурных групп и начального звена составляются и решаются уравнения статики. Причем на первом этапе находятся реакции во внешних кинематических парах, а затем во внутренних.
Для различных структурных групп (групп Ассура) разработаны специальные методы их силового исследования. Учитывая, что большинство современных механизмов, включая все механизмы, исследуемые при курсовом проектировании, содержат простейшие группы – диады, рассмотрим здесь только метод силового анализа этих групп.
Силовой анализ двухповодковых структурных групп проще проводить, используя метод разложения сил. Силы, приложенные во внешних вращательных кинематических парах, заменяются составляющими силами. Нормальная составляющая Fn обязательно направляется по линии, проходящей через центры двух вращательных пар. Если тангенциальная составляющая Ft приложена к одной из этих точек, то уравнение моментов, служащее для определения величины Ft, составляется относительно другой точки.
4.2.1. Силовой анализ структурной группы 4–5.
Начинаем
анализ с рассмотрения структурной группы 4–5, для чего рисуем структурную эту группу.
Прикладываем к ней с целью упрощения вычислений в проекциях на оси действующие
на нее силы. Действие на звено 5 со стороны стойки 0 заменяем реакцией R50y, а на звено 4 со стороны звена 3 – реакцией R43, которая раскладываем на
составляющие в проекциях на оси координат ![]() и
и
![]() . Чтобы не изображать отдельно звенья
4 и 5. В точке D прикладываем в проекциях
на оси реакцию R45.
. Чтобы не изображать отдельно звенья
4 и 5. В точке D прикладываем в проекциях
на оси реакцию R45.
1. Записываем в проекциях на ось координат х условие равновесия всех сил, действующих на структурную группу 4–5 в целом:
![]() , откуда
, откуда
![]()
2. Находим сумму моментов относительно точки D для звена 4
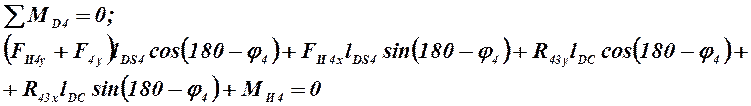 ,
,
откуда 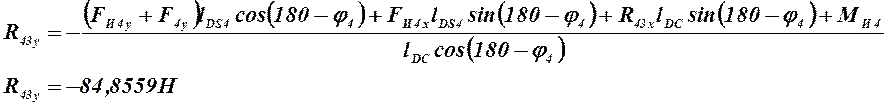
3. Запишем в проекциях на ось координат у условие равновесия всех сил, действующих на структурную группу 4–5 в целом:
![]() , откуда
, откуда
![]()
4. Находим сумму моментов относительно точки D для звена 5
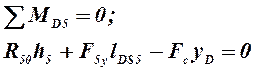
откуда 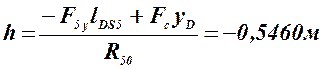
5. Записываем в проекциях на оси координат условия равновесия всех сил, действующих на звено 5:
![]() , откуда
, откуда ![]() .
.
![]() , откуда
, откуда ![]() .
.
Размеры длин звеньев берем из соответствующих планов положений.
![]()
Тогда
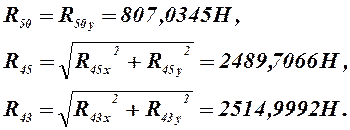
4.2.2. Силовой анализ структурной группы 2–3.
Помимо
заданных сил и сил инерции, на группу действуют реакции ![]() .
Силы представлены через и проекции на оси координат. Проекции R34x и R34y найдены из анализа
предыдущей группы:
.
Силы представлены через и проекции на оси координат. Проекции R34x и R34y найдены из анализа
предыдущей группы:
![]()
Для определения реакций в кинематических парах A и O2 записываем два уравнения проекций на оси и два уравнения моментов относительно точек О2 и А для звеньев 2 и 3:
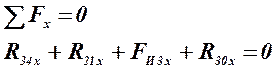 (4.2)
(4.2)
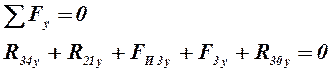 (4.3)
(4.3)
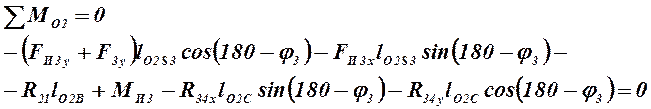 (4.4)
(4.4)
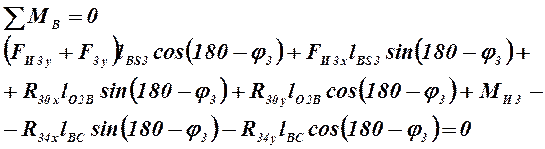 (4.5)
(4.5)
Далее из равенства (4.4) сразу можно найти величину вектора R21:
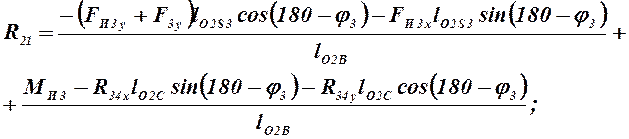
где длины звеньев берем из
соответствующего плана положений: ![]() Тогда
Тогда
![]()
Тогда для дальнейшего нахождения реакций можно определить проекции на координатные оси силы R21:
![]()
![]()
Далее из выше составленных уравнений (4.2) и (4.3) можно очень просто найти реакцию 3-его звена на опору
![]()
![]()
По теореме Пифагора найдем полную реакцию:
![]()
Для проверки правильности найденных значений можно подставить их в (4.5) и получить тождество.
4.2.3. Определение уравновешивающего момента My и реакции R10 в кинематической паре О1.
Для этого составляем уравнения равновесия начального звена механизма. Эти уравнения имеют следующий вид:
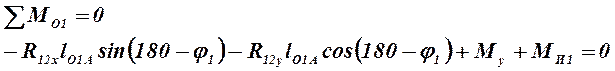
где ![]() ,
, ![]() ;
;
![]() ,
, ![]() –
проекции на оси координат реакции на звено 1 стойки 0;
–
проекции на оси координат реакции на звено 1 стойки 0; ![]() – длина первого звена;
– длина первого звена; ![]() – уравновешивающий момент.
– уравновешивающий момент.
Решая записанные выше уравнения, найдем
![]()
![]()
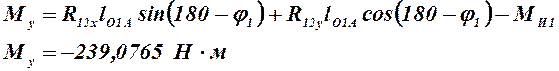
Полная реакция в опоре О1 будет определяться следующим образом:
![]() .
.
4.3. Определение уравновешивающего момента и реакций в кинематических парах графическим методом.
Силовой анализ графическим методом путем построения планов сил широко используется при исследовании механизмов. Это обусловлено не только их наглядностью, но и тем, что внешние силы, действующие на механизмы, практически всегда известны лишь приближенно. Поэтому точность графических решений обычно лежит в пределах допустимых норм.
4.3.1. Силовой анализ структурной группы 4–5.
Рисуем
структурную группу 4–5 и прикладываем к ней все
силы и моменты. Под действием приложенных сил и реакций структурная группа
находится в равновесии. Подлежат определению реакции R50 и R43 во внешних кинематических
парах, а также реакция ![]()
![]() во внутренней
кинематической паре D. Реакцию R43 изображаем разложенной на нормальную
во внутренней
кинематической паре D. Реакцию R43 изображаем разложенной на нормальную ![]() и касательную
и касательную ![]() составляющие соответственно.
составляющие соответственно.
Определим реакции R50 и R43 из условия равновесия звеньев 4–5. Для этого запишем векторное уравнение сил, действующих на эту группу в целом. Векторное уравнение записываем таким образом, чтобы неизвестные реакции находились по краям.
![]() . (4.6)
. (4.6)
Уравнение (4.6) решаем графическим методом построения планов сил. При черчении на альбомных листах необходимо было бы выбирать масштабный коэффициент сил, но в данном курсовом проекте для графических построений используется среда AutoCAD 14.0, где предусмотрена возможность автомасштабирования, то изображаем вектора сил в натуральную величину.
Последовательно,
начиная с Fc, откладываем на плане сил
векторы изображающие силы Fc, F5y, F4y, FИ4х, FИ4у и FИ5х. Из начала вектора Fс проводим вектор силы ![]() . Величину этого вектора можно найти, записав
сумму моментов относительно точки D для 4-ого звена.
. Величину этого вектора можно найти, записав
сумму моментов относительно точки D для 4-ого звена.
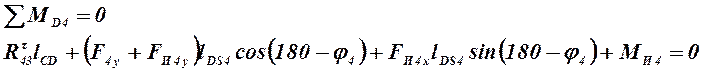 ,
,
откуда 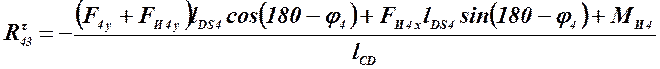
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.