Далее через
конец вектора ![]() проводим линию действия
силы
проводим линию действия
силы ![]() (вдоль 4-ого звена), а через
начало вектора FИ5х линию действия R50 до пересечения с линией
действия
(вдоль 4-ого звена), а через
начало вектора FИ5х линию действия R50 до пересечения с линией
действия ![]() . Таким образом, мы
графически решили векторное уравнение (4.6) и определили истинное значение
реакций R50 и
. Таким образом, мы
графически решили векторное уравнение (4.6) и определили истинное значение
реакций R50 и ![]() .
.
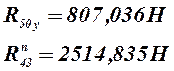
Суммируя
графически вектора ![]() и
и ![]() , находим полную реакцию
, находим полную реакцию ![]() .
.
![]()
Теперь определим реакцию в кинематической паре D. Для этого запишем векторное уравнение равновесия сил для 5-ого звена:
![]()
и построим план сил на
свободном поле чертежа. Истинная величина реакции ![]() .
.
Для определения точки приложения реакции R50 запишем сумму моментов относительно точки D для звена 5:
![]() .
.
Тогда 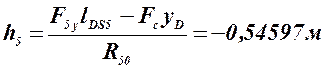
Результаты силового анализа структурной группы 4–5.
Величина |
R43, H |
R45, H |
R50, H |
h50, м |
|
Графически |
2514,9989 |
2489,7010 |
807,0360 |
-0,545971 |
|
Аналитически |
2514,9992 |
2489,7066 |
807,0345 |
-0,545972 |
|
Отклонение, D % |
-0,00001 |
-0,00022 |
0,00018 |
-0,00018 |
4.3.2. Силовой анализ структурной группы 2–3.
Рисуем
структурную группу 2–3 и прикладываем к ней все
действующие силы и моменты. Реакции ![]() и
и ![]() изображаем разложенными на нормальные и
касательные составляющие. В кинематической паре А возникает реакция 2-ого звена на 1-ое
изображаем разложенными на нормальные и
касательные составляющие. В кинематической паре А возникает реакция 2-ого звена на 1-ое ![]() , направленная перпендикулярно звену 3.
, направленная перпендикулярно звену 3.
Реакцию ![]() раскладываем на касательную
раскладываем на касательную ![]() и нормальную
и нормальную ![]() составляющие геометрически, то есть
составляющие геометрически, то есть ![]() .
.
Анализ структурной группы 2–3 проводим, основываясь на графическом решении уравнения
![]() (4.7)
(4.7)
Изображаем на
свободном поле чертежа последовательно вектора сил ![]() ,
, ![]() ,
, ![]() ,
,![]() и
и ![]() .
Далее для определения величины вектора
.
Далее для определения величины вектора ![]() запишем
сумму моментов относительно точки В:
запишем
сумму моментов относительно точки В:
 ,
,
откуда
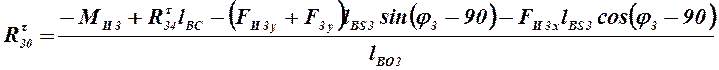
![]()
Затем из конца
вектора ![]() проводим вектор
проводим вектор ![]() , через конец которого проводим линию
действия силы
, через конец которого проводим линию
действия силы ![]() . После этого изобразив
линию действия силы
. После этого изобразив
линию действия силы ![]() до точки пересечения с
вышеуказанной линией, получим графическое решение векторного уравнения (4.7).
Сделав это, мы можем определить величины неизвестных ранее векторов
до точки пересечения с
вышеуказанной линией, получим графическое решение векторного уравнения (4.7).
Сделав это, мы можем определить величины неизвестных ранее векторов
![]()
![]()
Сложив
графически вектора ![]() и
и ![]() ,
найдем реакцию 3-его звена на опору:
,
найдем реакцию 3-его звена на опору: ![]() .
.
4.3.3. Силовой анализ начального звена.
Рисуем
начальное звено и прикладываем к нему все силы и моменты. Здесь Му – уравновешивающий
момент, а R12
= -R21. Раскладываем реакцию на 2-ое звено со стороны 1-ого R12 на составляющие касательную ![]() (перпендикулярную
1-ому звену), и нормальную
(перпендикулярную
1-ому звену), и нормальную ![]() (направленную вдоль исследуемого
звена).
(направленную вдоль исследуемого
звена).
Для определения реакции R10 в кинематической паре О1 запишем векторное уравнение сил, действующих на 1-ое звено:
![]() .
.
При построении плана сил для начального звена находим, что касательная и нормальная составляющие, действующие на опору со стороны 1-ого звена соответственно равны касательной и нормальной составляющих силы, действующей со стороны 2-ого звена на 1-ое, то есть
![]()
![]()
Запишем уравнение для суммы моментов относительно точки O1:
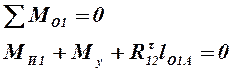 , откуда
, откуда
![]()
![]()
Составим таблицу сравнительного анализа аналитического и графического исследования структурной группы 2–3 и начального звена
Таблица 4.4.
Результаты силового анализа структурной группы 2–3 и начального звена.
Величина |
F21, H |
F30n, H |
F30, H |
F10, H |
My, Н×м |
|
Графически |
4178,3750 |
505,6450 |
1722,3590 |
4178,3750 |
-239,0766 |
|
Аналитически |
4178,3748 |
505,6428 |
1722,3592 |
4178,3748 |
-239,0765 |
|
Отклонение, D % |
0,00000 |
-0,00043 |
-0,00001 |
0,00000 |
0,00003 |
Теорема Н.Е. Жуковского применяется при решении многих задач динамики машин. В частности, она используется для определения уравновешивающего момента (уравновешивающей силы), если нет необходимости в последовательном определении реакций в кинематических парах механизма.
Теорема Жуковского гласит: «Если силу, приложенную к какой-либо точке звена механизма перенести параллельно самой себе в одноименные точки повернутого плана скоростей, то момент этой силы относительно полюса плана скоростей будет пропорционален ее мощности», то есть
![]() ,
,
где Mp – момент силы Fi относительно полюса плана скоростей, Pi – мощность силы Fi.
Из законов динамики следует, что сумма мощностей всех внешних сил и сил инерции звеньев, приложенных к механизму, равна нулю или
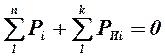 .
.
В соответствии с теоремой Жуковского последнее уравнение равносильно уравнению моментов относительно повернутого плана скоростей, то есть
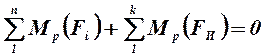 (4.8)
(4.8)
Из уравнения (4.8) и находится уравновешивающий момент (уравновешивающая сила).
Составим и решим (4.8) для исследуемого механизма поперечно-строгального станка. Строим повернутый на 90° градусов план скоростей механизма, к которому в соответствующих точках прикладываем заданные силы и силы инерции.
Моменты
инерции MИ1, MИ3 и MИ4 заменяются парами сил ![]() ,
, ![]() и
и ![]() соответственно, которые
прикладываем перпендикулярно отрезкам O1A, O2C и CD. В кинематических парах А, С и D модули этих сил
определяются
соответственно, которые
прикладываем перпендикулярно отрезкам O1A, O2C и CD. В кинематических парах А, С и D модули этих сил
определяются
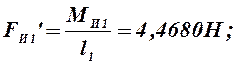
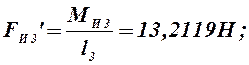
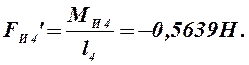
Все силы переносим в одноименные точки плана скоростей без изменения их направления. В точке А плана скоростей прикладываем неизвестную уравновешивающую силу Fy.
Записываем уравнение (4.8) моментов сил относительно полюса плана скоростей:
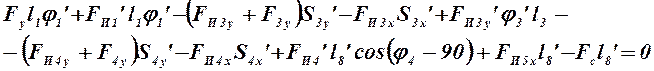 (4.9)
(4.9)
Так как на рычаге Жуковского силы показаны в условном направлении, то при составлении уравнения (4.9) их значения подставляем с учетом знака.
Решив (4.9), найдем силу Fy:
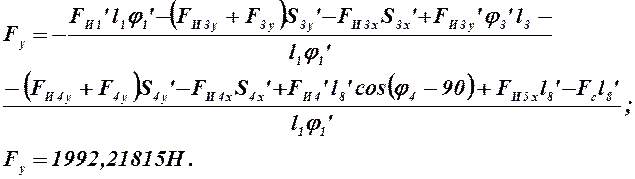
Зная величину Fy, найдем уравновешивающий
момент ![]() :
:
![]()
Отклонение
найденного с помощью рычага Жуковского значение момента ![]() от
определенного выше аналитическим методом
от
определенного выше аналитическим методом ![]() определится:
определится:
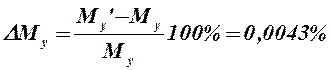 ,
,
что значительно меньше
допускаемого для инженерных расчетов значения ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.