














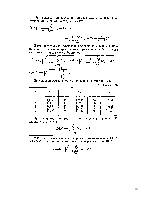

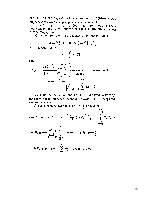

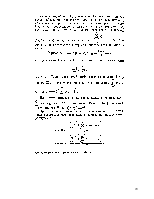
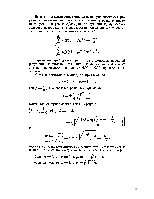















Лекция № 3
Введение в математическую статистику
· методы статистического анализа в оценке параметров моделей и их использования в системах управления; проверка статистических гипотез, алгоритмы дисперсионного, корреляционного и регрессионного анализа;
Для случайных процессов, а также в тех случаях, когда информации о рассматриваемом процессе недостаточно или процесс настолько сложен, что невозможно составить его детерминированную модель, прибегают к экспериментально-статистическим методам.
Процесс при этом рассматривают как «черный ящик».
Статистические методы могут быть применены всегда, но они не гарантируют адекватную оценку процесса!
?Можно ли использовать статистические методы для детерминированных процессов?
Задачи математической статистики состоят в том, чтобы на основании знания некоторых свойств подмножества элементов, взятых из некоторого множества, сделать какие-нибудь утверждения о свойствах этого множества, называемого генеральной совокупностью. В генеральной совокупности нас обычно интересует некоторый признак, который обусловлен случайностью и может иметь качественный или количественный характер.
Пример 1. Автомат производит валы. Множество всех валов, произведенных при определенных, остающихся неизменными производственных условиях, образует генеральную совокупность. Если интересующим признаком является, например, диаметр, то этот признак имеет количественный характер.
Пример 2. Поточная линия производит охотничьи патроны. Множество всех патронов, произведенных при некоторых остающихся неизменными условиях, составляет генеральную совокупность. Если нас интересует способность патрона функционировать или отказывать, то это качественный признак.
ГЕНЕРАЛЬНАЯ СОВОКУПНОСТЬ
Весь массив данных определенной категории называется генеральной совокупностью. Объем генеральной совокупности определяется задачами исследования.
Обычно генеральная совокупность включает очень большое число объектов изучаемой категории. Объем таких генеральных совокупностей считается равным бесконечности.
Иногда изучаются и небольшие генеральные совокупности, например группа животных, закрепленных за определенными работниками, с целью сравнения достижений этих работников. В таких случаях генеральной совокупностью будет совсем небольшое количество особей, которые все исследуются.
ВЫБОРКА
Выборка — это группа объектов, отличающаяся тремя особенностями:
1) это часть генеральной совокупности;
2) отобранная в случайном порядке, определенным образом;
3) исследуемая для характеристики как отобранных объектов, так и всей генеральной совокупности.
Для того чтобы 'по выборке можно было получить правильную характеристику всей генеральной совокупности, необходимо организовать правильный случайный отбор объектов из генеральной совокупности.
Тенденциозность, предвзятость три отборе объектов для выборочного исследования .препятствуют .получению правильных общих выводов, делают результаты выборочного исследования непоказательными для всей генеральной совокупности, т. е. нерепрезентативными.
Числовые характеристики групповых свойств для генеральной совокупности называются генеральными параметрами, а для выборок — выборочными показателями.
РЕПРЕЗЕНТАТИВНОСТЬ
Репрезентативность — это основное свойство выборочных групп характеризовать соответствующие генеральные совокупности с определенной точностью и достаточной надежностью.
ОШИБКИ РЕПРЕЗЕНТАТИВНОСТИ
Ошибки репрезентативности возникают только по одной причине: вследствие того, что целое характеризуется на основе исследований одной только части этого целого.
Ошибки репрезентативности нельзя смешивать с другими — организационными ошибками, допускаемыми иногда при проведении экспериментов, наблюдений и при анализе материалов производственной отчетности. Организационные ошибки это — методические ошибки, ошибки точности, ошибки внимания и ошибки типичности; обычно они могут быть устранены правильным и тщательным проведением исследования или во всяком случае могут быть сведены к минимуму.
Но организационные ошибки не могут быть ни учтены, ни обезврежены никакими математическими приемами обработки уже полученного первичного материала.
Ошибки репрезентативности резко отличаются от 'четырех видов организационных ошибок. Ошибки репрезентативности, во-первых, могут быть устранены статистическими методами и, во-вторых, не могут быть учтены при самой правильной и тщательной организации исследования (за исключением перехода на сплошное обследование генеральной совокупности).
При всей неизбежности ошибок репрезентативности их можно свести к минимуму путем привлечения в выборку достаточного числа объектов. Кроме того, величину ошибок репрезентативности можно определить с достаточным приближением на основе анализа выборочных данных и учесть при оценке генеральных параметров с требуемой точностью и надежностью.
Статистические методы учета ошибок репрезентативности дают возможность:
1) определять доверительные границы генеральных параметров и
2) определять достоверность выборочных разностей.
ДОВЕРИТЕЛЬНЫЕ ГРАНИЦЫ
Оценка генеральных параметров производится особым способом, в форме определения двух их возможных значений — минимально возможного и максимально возможного. Эти крайние значения, в пределах которых может находиться искомая величина генерального параметра, называются доверительными границами.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.