Процесс получения усредненного течения функции при равномерном увеличении аргумента называется выравниванием эмпирических рядов. В результате такого выравнивания на основе эмпирической ломаной линии получается усредненная .плавная теоретическая линия прямолинейной или криволинейной регрессии.
Эмпирический ряд регрессии это — двойной ряд цифр, включающих значения аргумента и соответствующие средние величины функции. При графическом изображении ряда регрессии аргумент откладывается по оси абсцисс, а функция — по оси ординат.
Процесс получения усредненного течения функции при равномерном усилении аргумента называется выравниванием эмпирических рядов. Выравнивание эмпирических рядов регрессии имеет большое и разностороннее .применение.
Способ скользящей средней
Если форма функции не известна, то сгладить случайные изломы эмпирической кривой -можно, применив способ простой скользящей средней. Этот способ заключается в том, что для каждого значения аргумента берут среднюю арифметическую из нескольких (соседних) значений функции.
Если скользящую среднюю берут по трем значениям аргумента, то складывают соседние значения функций для меньшего значения ар-тумента, для данного и для большего. Частное от деления этой суммы на три дает выравненное значение функции для данной величины аргумента.
Графический способ
Графический способ дает возможность с достаточным приближением получить теоретическую линию, а затем и теоретический ряд регрессии без каких-либо вычислений.
Наиболее простым оказывается применение графического способа к прямолинейной регрессии. В этих случаях на график наносят сначала эмпирическую линию регрессии, затем между крайними выступами ломаной эмпирической линии проводят прямую таким образом, чтобы сумма расстояний теоретической .прямой от точек эмпирической линии была бы наименьшей.
При известном навыке это можно сделать от руки, может помочь при этом натянутая нитка или прозрачная линейка с нанесенной прямой чертой. Натянутую нить располагают по среднему течению эмпирической линии и после нахождения наилучшего положения нитки на графике отмечают две крайние точки: для минимального и максимального значения аргумента. Теоретической линией регрессии будет прямая, соединяющая эти две точки.
По теоретической прямой можно определить числовые значения функции (ординаты), соответствующие определенным значениям аргумента (абсциссы).
Если регрессию нельзя считать прямолинейной, то графическое выравнивания эмпирической кривой также может быть проведено, но для этого необходимо иметь представление об общих закономерностях изменения функции.
Усложнение модели
математическая модель
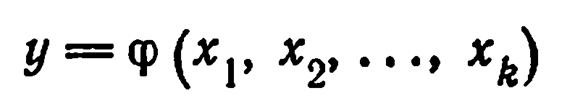представляется в виде
полинома — отрезка ряда Тейлора, в который разлагается неизвестная зависимость
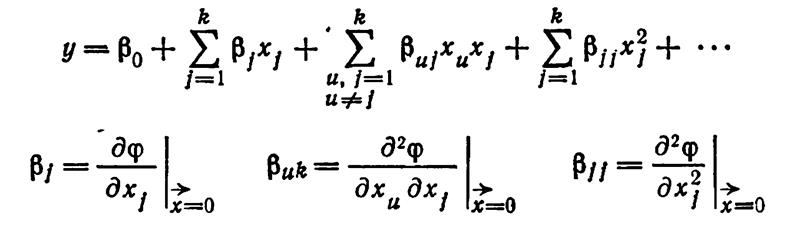
Уравнение регрессии, полученное на основании опыта:
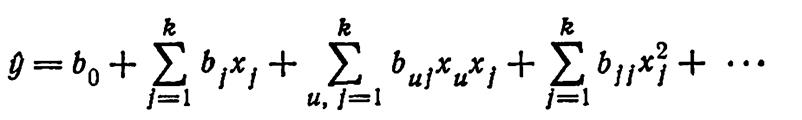
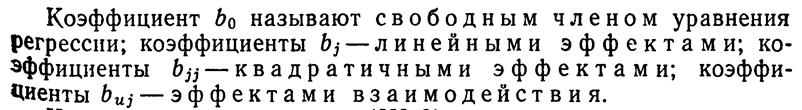
Способ наименьших квадратов
Наиболее общим аналитическим способом выравнивания эмпирических рядов регрессии служит способ наименьших квадратов. Этим способом «получаются такие выровненные значения функции, квадраты отклонения которых от эмпирических значений дают наименьшую сумму.
Этим способом можно выравнивать функции прямолинейные и криволинейные, простые и множественные.
Для оценки силы линейной связи вычисляется выборочный коэффициент корреляции:
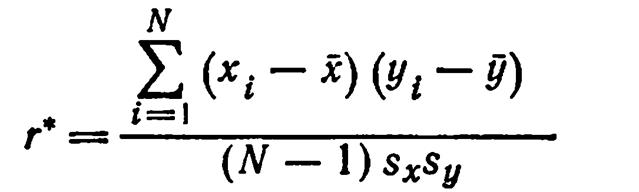
где sx, sy — выборочные среднеквадратичные отклонения.
Для линейного уравнения регрессии
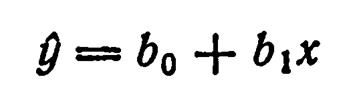
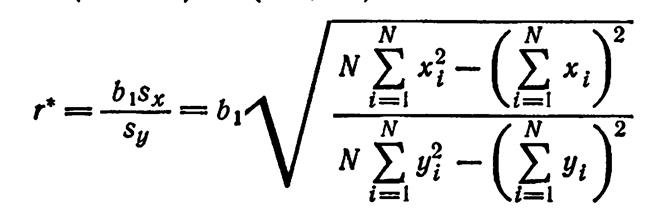
Лекция № 4
МЕТОДЫ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ
Методы планирования экспериментов позволяют свести к минимуму число необходимых опытов и одновременно выявить оптимальное значение искомой функции.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.