Введение в математическую статистику. Свойства точечных оценок. Способ скользящей средней, страница 2

НАДЕЖНОСТЬ

Надежность — это вероятность того, что генеральный .параметр действительно окажется внутри доверительных границ.

Критерий надежности определяется заранее, .при планировании исследования, исходя из .представления о большей или 'меньшей ответственности возможных результатов работы. Критерий надежности — это показатель вероятности безошибочных прогнозов.

Критерии Стьюдента используются при установлении доверительных границ генеральных .параметров и для определения достоверности разности.

ТОЧНОСТЬ

Точность — это степень приближения выборочного показателя к генеральному параметру при определенной надежности оценки.

Показатель точности, или ошибка репрезентативности выборочного показателя, определяется на основе выборочных данных по специальным формулам.

ДОСТОВЕРНОСТЬ

Достоверность — это особое свойство хорошо организованных выборок правильно отражать генеральные параметры.

Функции выборок. Пусть (Х₁, ..., Х_п) -математическая выборка. Случайная величина Z_n =Z(X₁, ..., Х_п) называется функцией выборки.

Пример.

Реализация 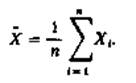  при конкретной выборке называется эмпирическим средним выборки (х₁ ..., х_n).

Пример.

Реализация 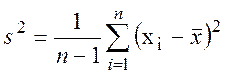называется   эмпирической   дисперсией выборки (х₁ ..., х_n).

Вопрос о распределении функции выборки является основной задачей математической статистики.

В случае малой выборки (п относительно мало) представляет интерес распределение функции выборки Z_n. В случае большой выборки (л велико) достаточно знать асимптотическое распределение Z_mт. е. предельное распределение Z_nпри п ®¥.

Не существует общего критерия, который позволял бы решить, когда выборка может считаться большой, а когда малой. В то время как распределение одной функции выборки уже при п = 30 можно с очень хорошим приближением заменить асимптотическим распределением, для другой функции выборки подобное приближение и при п = 100 все еще невозможно.

ОЦЕНКА ПАРАМЕТРОВ

В цехе на поточной линии изготовляются патроны для винтовок. Пусть вероятность того, что произвольно выбранный патрон негоден, равна р. Для того чтобы точно определить р, пришлось бы расстрелять все патроны, что не представляет собой разумного способа проверки.

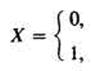если патрон годный, если патрон негодный.

Для оценки величины р делается выборка. Признак Xявляется качественным:

Тогда MX= 0*(1 -р)+ 1*р =p; таким образом, речь идет о том, чтобы оценить MXпри помощи сделанной выборки. Рассмотрим функцию выборки

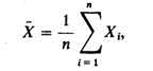
которая имеет значение относительной частоты негодных патронов в выборке объема п. Если (х₁ ..., х_n) — реализация выборки, то

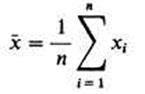
является, согласно закону больших чисел, приближенным значением неизвестного р. В общем случае задача оценки неизвестного параметра у (который как-либо связан с генеральной совокупностью, например,

у = MX) на основании выборки означает следующее. Нужно задать функцию выборки, реализация которой в некотором смысле могла бы рассматриваться как приближение у. Такая функция выборки называется точечной оценкой у.

Свойства точечных оценок.

Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру.

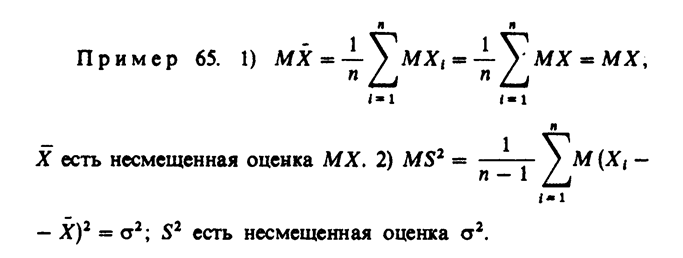
Математические модели

Математическая модель процесса это описание процесса математическими средствами (формулы, таблицы, номограммы), дающее возможность вскрыть внешнюю форму протекания процесса и получить дополнительную информацию о деталях процесса и о возможных его прогнозах.

Математическая модель показывает изменения функции при изменениях одного или нескольких аргументов (факторов).