Введение в математическую статистику. Свойства точечных оценок. Способ скользящей средней, страница 3

Функцией в данном случае называется признак, зависящий от другого признака — аргумента.

Если исследуется действие одного аргумента    (фактора), функция называется простой, а модель влияния — однофакторной:

Если исследуется действие нескольких   аргументов    (факторов), функция называется множественной, а модель — многофакторной:

МЕТОДЫ РЕГРЕССИОННОГО, КОРРЕЛЯЦИОННОГО и ДИСПЕРСИОННОГО АНАЛИЗА

Предположим, что мы имеем п наблюдений или измерений. В математических моделях наблюдения рассматриваются как п случайных величин y₁,…,y_n, которые являются линейными комбинациями с р неизвестными постояннымиплюс ошибки:

        (*)

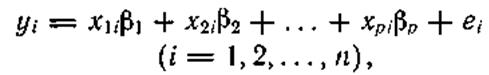где {x_ji} —известные постоянные коэффициенты*).

Наименьшие предположения о случайных величинах { е_i } состоят в том, что их математические ожидания равны нулю, т. е.

Кроме того, будем обычно предполагать, что

где s²— неизвестная постоянная, d_ij (символ Кронекера),_;- равно 0 или 1 при соответственно i¹jи i= j. Эти условия эквивалентны тому, что случайные величины нескоррелированы (т. е. их коэффициенты корреляции равны 0) и имеют одинаковые дисперсии, равные s².

Определения.

дисперсионный анализ — это статистический метод анализа результатов наблюдений, зависящих от различных одновременно действующих факторов, выбор наиболее важных факторов и оценка их влияния. Теория анализа результатов измерений подсказывает, как планировать проведение опыта или наблюдения, т. е. приводит к планированию эксперимента. Исторически современный метод дисперсионного анализа развивался главным образом в связи с приложениями к задачам сельского хозяйства.

Строгое определение: дисперсионный анализ— это система статистических методов обработки наблюдений, допускающих представление (*), где коэффициенты {x_ji}  являются целыми числами, равными обычно 0 и 1. Для того чтобы внести ясность в это определение, нужно не только указать возможные числовые значения {x_ji}, а нужно понять, какое место они занимают в описании задач, встречающихся в исследованиях. Эти .величины {x_ji}  имеют смысл «переменных-счетчиков», или «переменных-указателей», которые указывают присутствие или отсутствие влияний различных факторов {b_i } в условиях проводящихся наблюдений; x_jiобычно равно 0 или 1.

Величины {b_i} являются более или менее идеализированным -отражением некоторых сторон наблюдаемого явления, представляющих интерес для исследователя. Целью дисперсионного анализа является получение выводов относительно {е_i} и некоторых {b_i }, выводов, остающихся справедливыми независимо от значений других {b_i }, «исключить», которые было бы более желательно чем «оценивать».

Если {x_ji} не являются «переменными-указателями», а пробегают непрерывные множества значений, как, например, время t, температура (такие переменные называются независимыми, и тогда говорят, что {y_i}  являются наблюдениями зависимой переменной у), то мы получим регрессионный анализ. В случае, когда среди {x_ji} есть переменные двух видов, мы получаем ковариационный анализ.

Анализ на наличие связи между {x_ji} и {y_i}   называют корреляционным анализом.

РЕГРЕССИОННЫЙ АНАЛИЗ

Регрессией называется изменение функции в зависимости от изменений одного или нескольких аргументов. Для изображения регрессии используется: ряд регрессий (эмпирический и теоретический), линия регрессии, коэффициент регрессии и уравнение регрессии.

Рис. 1.   Эмпирическая   линия  

Графическое изображение течения функции в зависимости oт изменений аргумента называется линией регрессии.