Запишем ограничения, накладываемые связями на скорости точек механической системы. Для этого продифференцируем уравнения (1) вдоль движений механической системы. Тогда в совокупности с уравнениями (2) будем иметь:
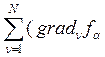 ,
,![]() +
+![]()
![]() ,
, ![]() , (3)
, (3)
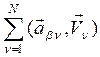 +
+![]()
![]() ,
, ![]() . (4)
. (4)
Определение 3.
Совокупность
векторов ![]() , являющаяся решением системы (3),(4)
при заданном возможном положении
, являющаяся решением системы (3),(4)
при заданном возможном положении ![]() в момент
в момент ![]() , называется
возможной скоростью механической системы в момент времени
, называется
возможной скоростью механической системы в момент времени ![]() в возможном положении
в возможном положении ![]() .
.
Если механическая
система свободная, то ее возможной скоростью в любом возможном положении
называется любая совокупность векторов ![]() .
.
Аналогично дается понятие возможного ускорения механической системы. Так же выписываются ограничения, накладываемые геометрическими и дифференциальными связями на ускорения:
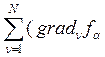 ,
,![]() +
+![]()
![]() ,…,
,…,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
, ![]() , (5)
, (5)
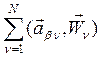 +
+![]()
![]() ,…,
,…,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,
, ![]() . (6)
. (6)
Здесь ![]() =
=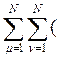
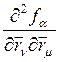
![]() ,
,![]() +
+![]()
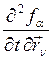 ,
,![]() +
+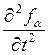 ,
,
![]() =
=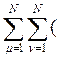
![]()
![]() ,
,![]() +
+![]()
![]() ,
,![]() +
+![]()
![]()
![]() ,
,![]() +
+![]() .
.
Компоненты векторов 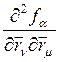
![]() ,
, 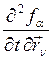 ,
, ![]()
![]() ,
, ![]() ,
, ![]() вычисляются
по формулам:
вычисляются
по формулам:
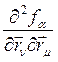
![]() =
=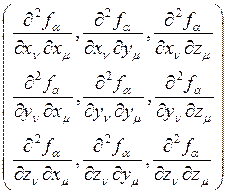
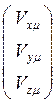 ,
, 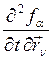 =
=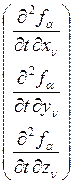 ,
,
![]()
![]()
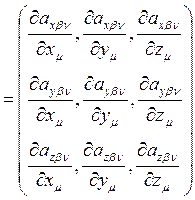
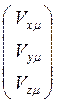 ,
, ![]()
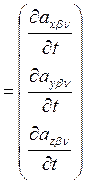 ,
, ![]()
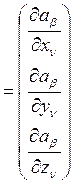 .
.
При
выводе формул (5) использовалось свойство равенства смешанных
производных при перестановке порядка дифференцирования, справедливое для дважды
непрерывно дифференцируемых функций ![]()
![]() ,...,
,...,![]() ,
,![]() ,
, ![]() .
.
Определение 4.
Совокупность
векторов ![]() , являющаяся решением системы уравнений
(5),(6) при заданных в момент
, являющаяся решением системы уравнений
(5),(6) при заданных в момент ![]() возможном положении
возможном положении ![]() и возможной
скорости
и возможной
скорости ![]() , называется возможным ускорением механической
системы в момент времени
, называется возможным ускорением механической
системы в момент времени ![]() .
.
2º. Действительные движения, положения, скорости и ускорения механической системы.
Определение 5.
Кинематически возможное движение называется действительным движением, если оно удовлетворяет аксиоматике Ньютона-Галилея, т.е. обращает уравнения Ньютона-Галилея в тождества.
Из определений 1-5 следует:
– всякое действительное движение — это возможное;
– не всякое возможное движение является действительным;
–
в любой момент времени ![]() положение, скорость и ускорение механической
системы, вычисленные на действительном движении, являются возможными.
положение, скорость и ускорение механической
системы, вычисленные на действительном движении, являются возможными.
Определение 6.
Положение,
скорость и ускорение механической системы, вычисленные на действительном
движении в момент времени ![]() , называются
действительными положением, скоростью и ускорением механической системы в этот
момент времени.
, называются
действительными положением, скоростью и ускорением механической системы в этот
момент времени.
3º. Возможные и действительные перемещения материальной точки и механической системы.
Пусть ![]() —
возможное движение материальной точки
—
возможное движение материальной точки ![]() . Тогда
в любой фиксированный момент времени
. Тогда
в любой фиксированный момент времени ![]() будем иметь:
будем иметь:
![]() —возможное положение точки
—возможное положение точки ![]() ;
;
![]() =
=![]() —возможную скорость точки
—возможную скорость точки ![]() ;
;
![]() =
=![]() =
=![]() —возможное ускорение точки
—возможное ускорение точки ![]() .
.
Пусть ![]() =
=![]() +
+![]() ,
, ![]() . Тогда
. Тогда ![]() —
возможное положение точки
—
возможное положение точки ![]() в момент
в момент ![]() +
+![]() .
.
Определение 7.
Вектор ![]() =
=![]() -
-![]() называется
возможным перемещением точки
называется
возможным перемещением точки ![]() за время
за время ![]() относительно
положения
относительно
положения
![]() .
.
Будем рассматривать возможные
перемещения ![]() точки
точки ![]() за время
за время ![]() при достаточно
малых значениях
при достаточно
малых значениях ![]() .
.
Тогда можем записать
![]() =
=![]()
![]() +
+![]()
![]() +
+![]() , где
, где 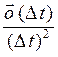 ——>0 при
——>0 при ![]() ——>0.
——>0.
Определение 8.
Вектор ![]() =
=![]() , где
, где ![]() — возможная скорость, имеющий своим
началом возможное положение
— возможная скорость, имеющий своим
началом возможное положение ![]() , называется возможным
линейным перемещением точки
, называется возможным
линейным перемещением точки ![]() за время
за время ![]() .
.
Очевидно, что если ![]() достаточно мало, то возможное перемещение
и возможное линейное перемещение точки
достаточно мало, то возможное перемещение
и возможное линейное перемещение точки ![]() совпадают
с точностью до членов порядка
совпадают
с точностью до членов порядка ![]() .
.
Определение 9.
Совокупность
векторов ![]() , где вектор
, где вектор ![]() определяется
по формуле
определяется
по формуле ![]() =
=![]() ,
, ![]() , и имеет своим началом возможное
положение
, и имеет своим началом возможное
положение ![]() точки
точки ![]() ,
называется возможным линейным перемещением механической системы за время
,
называется возможным линейным перемещением механической системы за время ![]() . Здесь
. Здесь ![]() —
возможная скорость точки
—
возможная скорость точки ![]() в момент времени
в момент времени ![]() в положении
в положении ![]() .
.
Выведем ограничения, накладываемые уравнениями связей на возможные линейные перемещения.
Воспользуемся уравнениями (3),(4), которым удовлетворяют возможные скорости точек механической системы.
Умножим каждое из них на ![]() .
Учитывая, что
.
Учитывая, что ![]() =
=![]() , придем
к следующим уравнениям, устанавливающим ограничения на возможные линейные
перемещения:
, придем
к следующим уравнениям, устанавливающим ограничения на возможные линейные
перемещения:
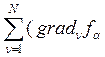 ,
,![]()
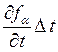
![]() ,
, ![]() , (7)
, (7)
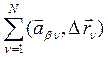 +
+![]()
![]() ,
, ![]() . (8)
. (8)
В матричной форме (7),(8) принимают вид
![]() +
+![]()
![]() , (9)
, (9)
где ![]() — матрица размерности
— матрица размерности ![]() ,
,
![]() — вектор-столбец
размерности
— вектор-столбец
размерности ![]() ,
,
![]() — вектор-столбец
размерности
— вектор-столбец
размерности ![]() ,
составленный из компонент векторов
,
составленный из компонент векторов ![]() ,
, ![]() .
.
В явном выражении матрица ![]() ,
вектора
,
вектора ![]() и
и ![]() представляются
следующим образом:
представляются
следующим образом:
![]()
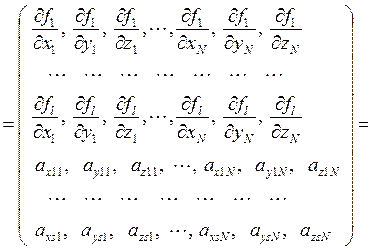
![]() . (10)
. (10)
В
блочной записи матрицы ![]() в (10) блоки
в (10) блоки ![]() и
и ![]() являются матрицами размерности
являются матрицами размерности ![]() и
и ![]() , соответственно:
, соответственно:
![]()
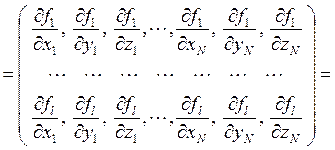
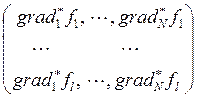 , (11)
, (11)
![]()
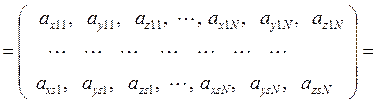
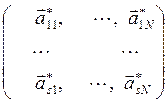 . (12)
. (12)
Векторы-столбцы ![]() и
и ![]() уравнения (9) в транспонированном виде
имеют следующее представление:
уравнения (9) в транспонированном виде
имеют следующее представление:
![]() (
(![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,…,
,…,![]() ),
),
![]()
![]() ,…,
,…,![]()
![]() ,…,
,…,![]() .
.
В этих формулах приняты обозначения:
— символ ![]() обозначает операцию транспонирования;
обозначает операцию транспонирования;
— для всех ![]() через
через ![]() ,
, ![]() ,
, ![]() обозначены векторы
обозначены векторы
![]() =
=![]() ,
,![]() ,
,![]() ,
, ![]() ,
,
![]()
![]() ,
, ![]() ,
,
![]()
![]() , где
, где
![]() ,
, ![]() ,
, ![]() — компоненты векторов
— компоненты векторов ![]() ,
,
![]() — компоненты векторов
— компоненты векторов ![]() в уравнениях (8),
в уравнениях (8),
![]() — компоненты векторов
— компоненты векторов ![]() (возможных линейных перемещений).
(возможных линейных перемещений).
Примечание 2.
Если в определениях 7,8,9 заменить возможное движение
действительным, то придем к понятиям действительного перемещения точки ![]() за время
за время ![]() ,
действительного линейного перемещения
точки
,
действительного линейного перемещения
точки ![]() за время
за время ![]() , действительного линейного перемещения механической системы
за время
, действительного линейного перемещения механической системы
за время ![]() .
.
Ограничения, накладываемые на действительные линейные
перемещения, будут иметь вид (7),(8),(9) с той лишь разницей, что коэффициенты
при ![]() и
и ![]() будут вычисляться в действительном положении механической
системы.
будут вычисляться в действительном положении механической
системы.
4º. Виртуальные перемещения механической системы.
Пусть в фиксированный момент
времени ![]() механическая система
механическая система
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.