Уравнения движения несвободных механических систем. Уравнения Лагранжа 1-го рода. Общее уравнение динамики и принцип Даламбера-Лагранжа. Уравнения Рауса в обобщенных координатах для неголономных систем

перемещений, допускаемых уравнениями связей (2),(3), то это значит, что для векторов , вычисленных по формуле (7), справедливо тождество

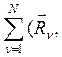
   для =Î.                   (8)

Данное заключение следует из того, что (6) является решением уравнения (5).

Соотношение (7) можем записать в виде

=+,     .                  (9)

Равенства (9) по форме совпадают с уравнениями (1), если  трактовать как силы, приложенные к точкам , . Для этих сил справедливы тождества (8). Отсюда делаем два вывода.

Первый вывод: для кинематически возможного движения (6), являющегося решением уравнения(5), справедливо уравнение(1); в нем силы , вычисляемые по формуле(7), удовлетворяют условиям идеальности.

Поскольку на кинематически возможное движение (6) не накладывалось никаких других условий, кроме требования быть решением уравнения (5), то из того, что на этом движении выполняется соотношение (9), можем сделать второй вывод: любое кинематически возможное движение, являющееся решением уравнения (5), будет решением уравнения (1).

Таким образом доказали следующее обратное утверждение.

Любое кинематически возможное решение уравнения (5) является действительным движением. Реакции связей, вычисляемые по формуле (7) на этом движении, удовлетворяют условиям идеальности.

Легко видеть, что если уравнение (5) имеет единственное кинематически возможное решение, то оно, согласно данному утверждению, будет единственным действительным движением. Таким образом, данное условие (условие существования единственного кинематически возможного решения уравнения (5)) является достаточным для существования единственного действительного движения.

Покажем, что данное условие является и необходимым для существования единственного решения уравнений Ньютона-Галилея. А именно, докажем, что из единственности решения уравнений Ньютона-Галилея при заданном начальном положении и начальной скорости механической системы следует единственность решения уравнения (5).

Доказательство проведем методом от противного. Итак, предположим, что существует два различных кинематически возможных решения уравнения (5) при заданных начальных условиях:

=,   =,   ,  при .

Тогда каждое из них, согласно доказанному выше, является действительным. Это значит, что два различных действительных движения проходят через заданное начальное положение и имеют одинаковую скорость в этот момент времени. Этот факт противоречит утверждению аксиомы 5 (принципу детерминированности Ньютона-Лапласа). Следовательно, наше предположение о неединственности решения уравнения (5) неверно.

Таким образом, справедлива следующая теорема, устанавливающая связь решений общего уравнения динамики и уравнений Ньютона-Галилея.

Теорема 1.

Для того чтобы кинематически возможное движение было действительным, необходимо и достаточно, чтобы оно было единственным решением уравнения (5) при заданных начальных условиях.

Замечание 1.

В теореме 1 доказательство необходимости существования единственного решения уравнения (5) проводилось на основе выполнении аксиомы 5.

Откажемся от аксиомы 5 в аксиоматике Ньютона-Галилея и заменим ее требованием, чтобы уравнение (5) при заданных начальных условиях имело единственное кинематически возможное движение. Легко показать, действуя по аналогии с доказательством, данным в теореме 1, что в этом случае уравнения Ньютона-Галилея будут иметь единственное решение задачи Коши и тем самым будет справедливо утверждение аксиомы 5.

Уравнение (5) получено для несвободных механических систем. Покажем теперь, что теорема 1 справедлива