Основные динамические характеристики движения. Количество движения. Главный вектор количества движения. Кинетическая энергия механической системы

Глава 4. Основные динамические характеристики движения.

§1. Количество движения. Главный вектор количества движения.

Будем рассматривать движения механической системы, состоящей из  точек  с массами . Пусть  и = — положение и скорость точки , .

Определение 1.

Вектор =называется вектором количества движения материальной точки  или ее импульсом.

Импульс материальной точки имеет относительный характер. В зависимости от того, по отношению к какой системе координат рассматривается ее движение, по отношению к этой системе координат и рассматривается импульс.

Определение 2.

Вектор называется главным вектором количества движения механической системы. Здесьсуммирование векторов  проводится по правилу суммирования свободных векторов.

Вектор  иногда называют просто количествомдвижения системы.

Примечание.

На все формулы этой главы, содержащие символ суммирования по , распространяется Примечание 2 из §1 главы 3.

Теорема1.

   Справедлива формула =, где  — скорость центра масс,  — масса всей системы.

Доказательство.

Из определения центра масс имеем =. Дифференцируя по , получим требуемое            =.

Следствие 1.

Если центр масс в какой-либо системе координат сохраняет неизменным свое положение, то количестводвижения относительно этой системы координат равно нулю.

Доказательство.

Действительно, если  обозначает положение центра масс в системе координат, относительно которой он неподвижен, а  — положение материальной точки , , в этой системе, то будем иметь

.                             (1)

Сама система координат может быть подвижной или неподвижной относительно инерциального пространства. Однако, дифференцируя (1) условно в указанной системе координат и учитывая, что в этой системе =, получим

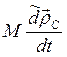
=.                     (2)

Следствие доказано.

Примеры.

1.  В твердом теле центр масс сохраняет свое положение неизменным. Поэтому имеем . Здесь  — количестводвижения твердого тела относительно связанной системы координат.

2.  Твердое тело вращается вокруг неподвижной оси, проходящей через центр масс. Поскольку центр масс неподвижен в абсолютном пространстве, то будем иметь . Здесь  — количестводвижения твердого тела в абсолютном пространстве.

3.  Твердое тело вращается вокруг неподвижной точки, совпадающей с центром масс. Здесь, как и в предыдущем примере, центр масс неподвижен в абсолютном пространстве. Поэтому . Как и выше,  —количестводвижения тела в абсолютном пространстве.

§2. Кинетический момент системы материальных точек.

1º. Понятие кинетического момента системы материальных точек.

В заданном пространстве (подвижном или неподвижном) фиксируем некоторую точку . Точка  может двигаться относительно этого пространства или оставаться неподвижной. Обозначим = — радиус-вектор материальной точки  механической системы относительно точки .

Определение 1.

Кинетическим моментом точки , или иначе, моментом количества движения точки, относительно точки  называется вектор

==.

Здесь  — импульс точки  относительно заданного пространства.

Определение 2.

Кинетическим моментом точки , или иначе, моментом количествадвижения точки, относительно оси  называется проекция на ось  кинетического момента материальной точки относительно центра , взятого на данной оси.

Как и в случае определения момента силы относительно оси, легко убедиться, что кинетический момент относительно оси  не зависит от выбора центра  на этой оси.

Определение 3.

Кинетическим моментом системыматериальных точек относительно центра  (главным моментом количества движения относительно центра ) называется вектор

===.

Определение 4.

Кинетическим моментом системыматериальных точек, или иначе, главным моментом количествадвижения, относительно оси  называется проекция