Сложное движение. Сложное движение материальной точки. Кинематические уравнения Эйлера. Задача Дарбу. Кинематические уравнения Пуассона

определению 3 называется переносным движением в задаче о сложном движении точки.

Если фиксировать какое-либо одно значение  в системе отсчета , то вектор-функция  выделяет из семейства (9) движение в абсолютном пространстве той точки , которая занимает неизменное положение = в подвижном пространстве.

Определение 4.

Переносным движением точки  называется абсолютное движение точки  фиктивного твердого тела, с которой по своему положению в момент времени  совпадает точка .

Из определения 4 вытекает, что переносное движение точки  задается равенствами (8)-(9), в которых следует положить =, где  = — фиксированное в момент времени  положение точки  в системе отсчета . Иначе говоря, переносное движение точки  определяется по формуле

==.                     (10)

В вектор-функции  от времени  зависят только  и матрица ориентации , а вектор  остается неизменным. Слева стоит вектор =, которым устанавливается положение точки  в абсолютном пространстве, задаваемое ее переносным движением.

Определение 5.

Абсолютное движение точки , задаваемое ее переносным и относительным движением, называется сложным движением этой точки.

Основная задача кинематики сложного движения:

–  установить связь между абсолютным движением и движениями переносным и относительным;

–  установить связь между кинематическими характеристиками указанных движений.

Движения переносное и относительное называются составляющими сложного движения материальной точки.

2º. Связь между составляющими движениями в сложном движении     материальной точки.

Найдем связь между абсолютным, переносным и относительным движением материальной точки. Для этого сначала рассмотрим абсолютное движение  материальной точки . Будем определять его через движение , задаваемое относительно точки отсчета . Пусть точка  в момент времени  занимает положение =. Положение точки  в этот же момент времени  относительно точки отсчета  обозначим через  (см. рис.2).

 

 

      

             

                Рис.2.

Если = — положение точки отсчета  в момент  относительно точки отсчета , то по правилу сложения векторов можем записать

=+, или иначе

==+.                      (11)

В координатной форме это векторное соотношение примет вид:

=, где       , ,     — координаты вектора ,

, ,   — координаты вектора ,

, ,     — координаты вектора .

Координаты всех векторов задаются в абсолютной системе координат.

Будем теперь рассматривать положение точки  в этот же момент времени  относительно точки отсчета  в подвижном пространстве. Это положение задается вектор-функцией , т.е. имеем

==.                             (12)

Вектор-функция  определяет относительное движение точки . В координатной форме равенство (12) примет вид:

.

Здесь ,,         — координаты точки  в момент времени  в подвижной системе координат , или иначе, это координаты вектора ;

, ,   — координатные функции относительного движения

в подвижной системе координат .

Поскольку = и =, то можем записать

=.                              (13)

Векторы  и  задаются в разных системах координат. В координатной форме равенство (13) выполняется в каждый момент времени  и имеет вид:

.

Здесь  — вектор-функции, задающие движение базиса подвижного пространства  в абсолютном .

Если  — матрица ориентации пространства  относительно пространства  в момент времени , то можем записать

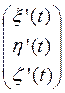=, или иначе,

=.                             (14)

Поэтому, подставляя (14) в (11), получим

=+,                           (15)

где                      =.                   (16)

В (15) слева стоит вектор-функция, определяющая абсолютное движение точки , а справа — функция, записанная в векторно-матричной форме, задающая движение некоторого фиктивного твердого тела. Для него связанной системой координат служит подвижная система . В (15) условно следует считать вектор  неподвижным в системе . Этот вектор совпадает с тем положением точки  твердого тела, которое занимает в нем в момент времени  точка .

В (16) слева стоит вектор , указывающий в момент времени  положение точки  в фиктивном твердом теле. Справа в (16) стоит вектор-функция , задающая относительное движение точки . Следовательно, равенство (15) означает, что абсолютное движение точки  (левая часть равенства (15)) совпадает с движением той точки  фиктивного твердого тела (правая часть равенства (15)), с которой в момент времени  по положению совпадает материальная точка .

По определению 4 переносного движения точки  векторная функция, стоящая справа в (15), — это функция, задающая переносное движение указанной точки (см. (10)).

Равенство (16) (по определению 1) — это относительное движение точки .

Таким образом, соотношения (15) и (16) устанавливают связь между абсолютным, переносным и относительным движением точки .

Подставляя (16) в (15), получим эту связь в виде одного равенства, записанного в векторно-матричной форме

=.                      (17)

В (17)  задается координатными функциями в подвижных осях