Главный вектор и главный момент системы сил. Силовое поле. Силовая функция. Потенциал. Идеальные связи. Аксиома идеальности связей. Примеры идеальных связей

§7. Главный вектор и главный момент системы сил.

1º. Главный вектор системы сил.

Обозначим через  равнодействующую системы сил, приложенных к точке , .

Определение 1.

Главным вектором системы сил ,…,, приложенных к материальным точкам механической системы, называется вектор

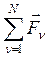=.                            (1)

Здесь сумма строится по правилу суммирования свободных векторов.

Из определения 1 вытекают следующие свойства главного вектора.

1.  Главный вектор — это свободный вектор.

2.  Координаты  через координаты составляющих сил  вычисляются по формулам

=,       =,       =.

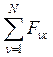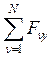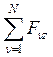Теорема 1.

Главный вектор внутренних сил механической системы равен нулю:

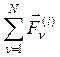
=.                        (2)

Утверждение справедливо, ибо из аксиомы 3 для внутренних сил (сил взаимодействия любых двух точек системы) можем записать

=.

Вычислим сумму (1) внутренних сил, объединяя пары взаимодействующих между собой точек. Тогда получим (2).

2º. Момент силы относительно точки и его свойства.

Пусть сила  приложена к точке . Фиксируем произвольную точку .

Определение 2.

Моментом силы  относительно точки  называется вектор

=,

где = — радиус-вектор точки  приложения силы относительно точки  (рис. 1).

Момент обозначается  или .

                     =

    =

                                                

           

                               =

     

      

Рис.1.                        Рис.2.

Отметим основные свойства момента силы относительно точки , вытекающие из определения 2.

1.   ортогонален плоскости, проходящей через точку  и линию действия силы .

2.  Векторы ,  и  образуют правую тройку векторов.

3.  =, где  — расстояние от точки  до линии действия силы  (рис.1); оно называется плечом силы.

4.   не изменяется, если в качестве начала (точки приложения) силы взять любую другую точку на линии действия силы .

Действительно, пусть (рис. 2)  и  — две точки на линии действия силы . Обозначим  — силу , приложенную к точке , а  — силу , приложенную к точке . Тогда можем записать ==.

Пусть ,  — момент силы относительно точки . Тогда по определению         =,     =.

Покажем, что =. Поскольку =+ и вектор  коллинеарен , то

=(+)=+.

Второе слагаемое равно нулю, так как  коллинеарен .

Векторы  и  имеют одинаковую длину, лежат на одной прямой и имеют одинаковое направление. Но тогда

==.

А потому                   =.

Из этого свойства вытекает, что силу можно переносить вдоль линии действия, и при таком переносе момент силы относительно точки  не изменится. Это значит, что сила  является скользящим вектором по отношению к операции вычисления момента.

5. Если силы  и  приложены к одной точке или если они приложены к разным точкам, но их линии действия совпадают либо пересекаются, то справедлива формула

=+.

Здесь под суммой  понимается равнодействующая сил  и , приложенных к точке пересечения их линий действия, если эти линии пересекаются, и приложенных к любой фиксированной точке на их линии действия, если эти линии совпадают.

6. Для того чтобы было , необходимо и достаточно, чтобы точка находилась на линии действия силы, либо сила .

3º. Момент силы относительно оси и его свойства.

Пусть задана ось «» с направляющим ортом  и пусть  — некоторая точка на этой оси.

Определение 3.

Моментом силы  относительно оси называется ортогональная проекция на эту ось момента данной силы , вычисленного относительно какой-либо фиксированной точки, взятой на оси (например, относительно точки ).

Момент силы относительно оси обозначают  либо . Отметим следующие свойства момента силы относительно оси «», вытекающие из его определения.

1. Если  — направляющий орт оси «», то =.

2.  — это скалярная величина.

3.  не зависит от выбора точки на оси «».

Действительно, пусть  и  — точки, лежащие на оси «». По определению 2

=,       =.

Обозначим  — момент силы  относительно оси «», вычисленный по точке , а  — момент силы , вычисленный по точке . Тогда по определению 3

=,        =.

Поскольку =+, и вектор  коллинеарен  (рис.3), то

==+.

                          

                             

 

     

     Рис.3.

Первое слагаемое равно нулю, так как  и  коллинеарны. Получили требуемое:

=.

4. Пусть ось «» проходит через полюс  декартовой прямоугольной системы координат и  — координаты орта ;  — координаты точки  приложения силы ; — координаты силы . Тогда

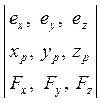=.                       (3)

Если ось «» не проходит через полюс  декартовой прямоугольной системы координат и  — координаты какой-либо точки , лежащей на этой оси, то

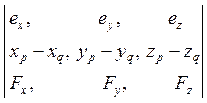=.                  (4)

Соотношения (3) и (4) для  получаются из формулы связи смешанных произведений  и  с декартовыми координатами входящих в них векторов. В этих произведениях , .

5. Момент силы относительно оси не зависит от выбора точки приложения силы на линии ее действия.

Утверждение справедливо, так как момент  не зависит от выбора точки приложения силы  на линии действия.

6. Если силы  и  приложены к одной точке или если они приложены к разным точкам, но их линии действия совпадают либо пересекаются, то справедлива формула

.

Здесь под суммой  понимается равнодействующая сил  и , приложенных к точке пересечения их линий действия, если эти линии пересекаются, и приложенных к любой фиксированной точке на их линии действия, если эти линии совпадают.

Для того чтобы было , необходимо и достаточно, чтобы ось «» и линия действия силы  находились в одной плоскости; иначе говоря, ось «» и линия действия силы  расположены следующим образом:      а) параллельны;      б) пересекаются;      в) совпадают.

Утверждение очевидно.

7. Момент силы  относительно точки  (полюса декартовой прямоугольной