Геометрия масс. Центр масс механической системы. Момент инерции. Главные оси инерции и главные моменты инерции

направление и величина), который подчиняется общему правилу пересчета положения любой геометрической точки при переходе к другой точке отсчета.

2. Пусть  — система отсчета. Тогда координаты центра масс в этой системе, как следует из (1), задаются соотношениями:

=,        =,        =.

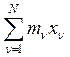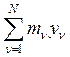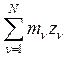3. Пусть  — система отсчета с полюсом в точке ,  — матрица перехода от системы  к системе , , ,  — координаты точки  в системе , , ,  — координаты центра масс в системе . Тогда справедливы соотношения

=+,

=,        =,   =.

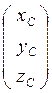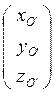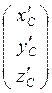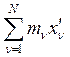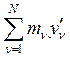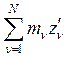4. Если точки  неподвижны в системе , то при движении механической системы координаты , ,  этих точек будут оставаться постоянными. А тогда, согласно (2), центр масс в системе  будет неподвижным.

5. Если за полюс системы  взять точку , то

º

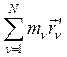
при любых движениях механической системы.

2º. Момент инерции относительно оси.

Пусть задана ось , проходящая через точку отсчета ; = — радиус-вектор точки  механической системы относительно точки отсчета ,  (см. рис.1).

                        Обозначим

               — расстояние от точки  до оси ,

                           — масса точки ,

                                — орт направляющего вектора оси .

             

  Рис.1.

Определение 2.

Моментом инерции точки  относительно оси  называется величина , задаваемая формулой                                             =.

Определение 3.

Моментом инерции механической системы относительно оси  называется величина, задаваемая формулой

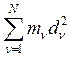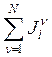==.                    (5)

Определение 4.

Величина 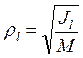                                              (6)

называется радиусоминерции механической системы относительно оси .

Из (6) следует, что

=,        .

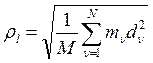Легко видеть (см. рис.1), что

==, или иначе,  =.

Поэтому, подставляя  в правую часть равенства (5), получим

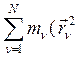
=.                      (7)

Примечание 2.

Если в качестве механической системы рассматривается твердое тело, то все формулы, встречающиеся в этой и последующих главах, в которых участвует масса  материальной точки  и применяется суммирование по индексу , должны рассматриваться с заменой  на элементарную массу , которая занимает в теле положение  или в абсолютном пространстве положение .

После такой замены в этих формулах суммирование по  должно быть заменено интегрированием по всей массе твердого тела. В частности, если известна плотность твердого тела, то алгоритм замены подробно был описан выше в примечании 1 к определению 1 на примере понятия центра масс.

С учетом данного примечания в дальнейшем не будем указывать в пределы изменения индекса суммирования, имея в виду, что для механических систем с конечным числом материальных точек он меняется от 1 до , а для твердого тела суммы заменяются интегралами.

Отметим свойства момента инерции относительно оси.

1. , , т.е. момент инерции и радиус инерции — неотрицательные числа. Величины , , тогда и только тогда, когда все точки механической системы находятся на оси .

2. Если в какой-либо системе координат при движении механической системы расстояние от каждой материальной точки системы до оси не изменяется, то момент инерции такой системы относительно этой оси остается постоянным. В частности, для твердого тела — если ось  неподвижна в твердом теле, то =. Следовательно, моменты инерции твердого тела относительно связанных осей постоянны на любых его движениях.

3. Дадим другое представление момента инерции  в зависимости от направляющего орта , отличающееся по форме от (7).

Пусть ось  проходит через начало координат в системе . Обозначим  — координаты точек механической системы,  — направляющие косинусы орта  в этой системе координат.

Обратимся к формуле (7). Запишем ее в алгебраической форме. Для этого обозначим

=,        =.

Легко видеть, что

=,      =.

Подставляя  и  в правую часть (7), будем иметь

=()()].

Заменим произведения  и  следующими очевидными представлениями

,     .

В них  обозначает единичную матрицу третьего порядка.

После подстановки их в  придем к выражению

, которое запишем в следующей форме

=,                          (8)

где  .

Отметим основные свойства матрицы .

1. Матрица  не зависит от координат орта , т.е. не зависит от выбора оси .

2. Значения элементов матрицы  существенно зависят от того, в какой системе координат задаются векторы . Иначе говоря, матрица  зависит от выбора системы отсчета, в которой задаются координаты векторов .

3. Для вычисления момента инерции  по формуле (8) необходимо, чтобы элементы матрицы  и вектора  были заданы в одной и той же системе координат, а ось  проходила через точку .

4. Момент инерции  является квадратичной формой относительно компонент вектора . Матрица коэффициентов этой квадратичной формы совпадает с матрицей .

§2. Тензор инерции и его свойства.

Определение 1.

Матрица , определяемая по формуле

                       (1)

и обладающая следующими свойствами:

1)  элементы ее задаются в той системе координат с полюсом , в которой определены координаты векторов ;

2)  для нее справедливы операции линейной алгебры только в тех случаях