Синтез систем адаптивного управления на основе метода вектора скорости. Расчет и анализ свойств многоканальной адаптивной системы. Определение структуры адаптивного регулятора

Чтобы усовершенствовать ум, надо

больше размышлять, чем заучивать. (Р. Декарт)

4. СИНТЕЗ СИСТЕМ АДАПТИВНОГО УПРАВЛЕНИЯ НА ОСНОВЕ МЕТОДА ВЕКТОРА СКОРОСТИ

Адаптивные системы управления, синтезированные на основе метода вектора скорости, также относятся к классу систем с эталонными моделями, как и рассмотренные ранее. На примере этих систем показано, какие новые алгоритмы и свойства можно получить, если использовать полный вектор первых производных координат состояния.

4.1 Расчет и анализ свойств многоканальной адаптивной системы

Стабилизация динамических характеристик систем с  непрерывными нестационарными объектами осуществляется с помощью нелинейного адаптивного регулятора, синтез которого выполнен на основе метода вектора скорости [8].  В процессе работы системы собирается и анализируется априори неизвестная информация о свойствах объекта управления. Основным источником такой информации являются производные выходной переменной или вектор первых производных координат состояния. Полученная информация используется в адапторе для изменения значений коэффициентов регулятора. Это позволяет создать «быстрый» адаптор для парирования быстроменяющихся возмущений.  Оценивание требуемых производных осуществляется с помощью малоинерционного линейного фильтра (ФОП). Применение АН также возможно, но в тех случаях, когда возмущения меняют достаточно медленно, а начальные условия в объекте ненулевые.

4.1.1  Описание задачи

Рассмотрим класс нестационарных нелинейных объектов, модель которых  в пространстве состояний  имеет вид:

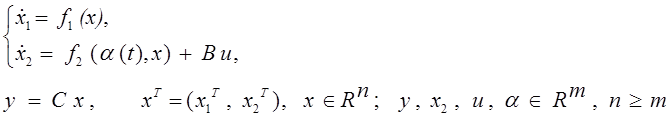 (4.1)             где y, x, u, a - соответственно векторы выходных переменных, координат состояния, управляющих воздействий, неконтролируемых возмущений, f₁ - известная, ограниченная, непрерывно дифференцируемая вектор - функция, f₂ - взаимооднозначная, непрерывно дифференцируемая по всем аргументам вектор - функция, компоненты которой и частные производные по a, x      ограничены. В общем случае f₂  может иметь гладкие нелинейности, но должно выполняться требование линейности по неизвестным параметрам;  С и  В -  известные матрицы коэффициентов,  det (CB)¹0. Считаем, что подсистема устойчива. Кроме того, известно, что a (t) принадлежит огра-ниченному нестационарному множеству значений a (t) ÎW^m, в котором  a_j (t) удовлетворяют условию

       (4.2)

где   h _j - известны; причем элементы вектора неконтролируемых возмущений могут  менять знак, что в случае параметрических возмущений приводит к потере устойчивости объекта. Темп неконтролируемых возмущений может быть соизмерим с темпом переходного процесса.

Цель управления состоит в переводе системы из произвольных начальных условий в допустимую ограниченную область относительно заданного состояния, независимо от действия неконтролируемых возмущений. Перевод объекта из любых начальных условий (y (t₀)) в заданную точку пространства выходных переменных должен осуществляться в соответствии с уравнением

                                                         (4.3)

независимо от действующих возмущений; F - вектор-функция, описывающая желаемые динамические свойства по выходным переменным, r- вектор уставок, rÎ R^m, r = const.

4.1.2  Определение структуры адаптивного регулятора

Нетрудно показать, что  для рассматриваемого класса объектов поставленная задача имеет решение, если выполняются условия:

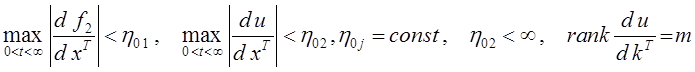, где k - вектор настраиваемых коэффициентов регулятора. Таким образом, дополнительно к условиям, определяющим класс рассматриваемых объектов, требуется ограниченность области допустимых значений переменных состояния, коэффициентов регулятора.

На начальном этапе синтеза определяется структура регулятора. Переходные процессы в адаптивной системе должны подчиняться (4.3). Определим вектор первых производных выходных переменных, дифференцируя уравнение выхода в (4.1):

где . Теперь приравняем правые части полученного уравнения и уравнения (4.3). Разрешив это равенство относительно вектора управляющих воздействий, получим

                  (4.4)

где k - вектор настраиваемых коэффициентов регулятора, kÎR^m  , причем .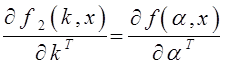

Далее выбирается алгоритм настройки коэффициентов регулятора, который, в общем случае,  можно  записать в виде

где Y- нелинейная вектор - функция. В дальнейшем будем рассматривать алгоритмы, полученные на основе метода вектора скорости, а именно:    

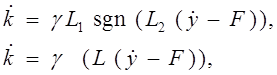                                                                     (4.5)

где  g = diag{ g₁ ,..., g_m }  - матрица коэффициентов передачи, L, L₁, L₂ - вспомогательные матрицы, элементы которых зависят от координат состояния,

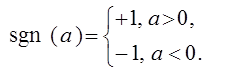
Значения g и вид L, L₁, L₂ определяются из  условия сходимости процессов к желаемой траектории. Изменение коэффициента регулятора направлено на уменьшение рассогласования между  и  F. Использование информации о векторе производных выходных переменных позволяет говорить о том, что вариации параметров объекта достаточно быстро будут парироваться коэффициентами регулятора.

4.1.3  Сходимость процессов к желаемой траектории

Исследование устойчивости системы с разрывным алгоритмом адаптации проведено на основе аналога теоремы Ляпунова для систем со скользящими режимами [28]. Выполним анализ функции в виде квадратичной формы