![]() , где
, где ![]() ,
полная производная по времени которой имеет вид
,
полная производная по времени которой имеет вид ![]() здесь использованы следующие
обозначения
здесь использованы следующие
обозначения 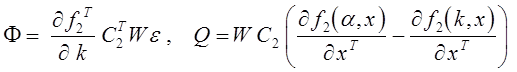 . Из условия
. Из условия ![]() выбираем
выбираем ![]() , т.е.
, т.е. 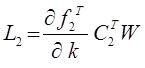 , а
, а ![]() . Если
. Если ![]() для любого момента времени, то производная
рассматриваемой функции будет отрицательно определенной (
для любого момента времени, то производная
рассматриваемой функции будет отрицательно определенной (![]() ). С учетом (4.2), получаем следующие
условия на значения элементов матриц
). С учетом (4.2), получаем следующие
условия на значения элементов матриц ![]() и g:
и g:
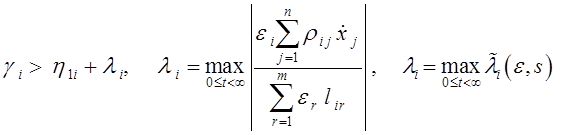 (4.6)
(4.6)
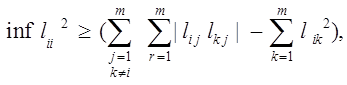
![]() (4.7)
(4.7)
причем элементы ![]() - зависят от рассогласования между
соответствующими компонентами векторов a и k, (
- зависят от рассогласования между
соответствующими компонентами векторов a и k, (![]() ). Таким образом,
величина λi определяется, в основном, координатными (εi) и параметрическими
рассогласованиями.
). Таким образом,
величина λi определяется, в основном, координатными (εi) и параметрическими
рассогласованиями.
С помощью функций
Ляпунова также определяется оценка времени сходимости процессов к желаемой
траектории. Основная идея способа изложена в [28, 31]. В [32] показано, что
время сходимости процессов в системе стабилизации с производными в законе
адаптивного управления конечно и зависит от координатных и параметрических
рассогласований в начальный момент времени, а также от коэффициента передачи
адаптора. Требуемые оценки координат состояния и элементов вектора ![]() могут быть получены с помощью линейного
фильтра оценки производных (или наблюдателя состояния) [7].
могут быть получены с помощью линейного
фильтра оценки производных (или наблюдателя состояния) [7].
Пример 4.1. Выполним расчет двухканальной адаптивной системы. Пусть динамика объекта описывается уравнениями:
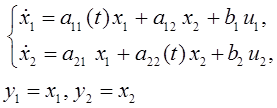
где ![]() -
неизвестные переменные, а
-
неизвестные переменные, а ![]() -постоянные
коэффициенты, i ≠ j.
-постоянные
коэффициенты, i ≠ j.
Определение параметров эталонной модели
осуществляется по желаемым корням характеристического полинома, область
допустимого расположения которых вычисляется на основе показателей качества
переходного процесса (перерегулирования
- ![]() , времи переходного процесса по каналам -
, времи переходного процесса по каналам - ![]() , величине установившейся ошибки -
, величине установившейся ошибки - ![]() ):
):
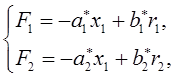
где параметры
![]() имеют следующие значения:
имеют следующие значения: ![]() ;
; ![]() ;
; ![]() – входные воздействия. Тогда уравнения
замкнутой системы, полученные в соответствии с изложенной методикой, имеют вид:
– входные воздействия. Тогда уравнения
замкнутой системы, полученные в соответствии с изложенной методикой, имеют вид:
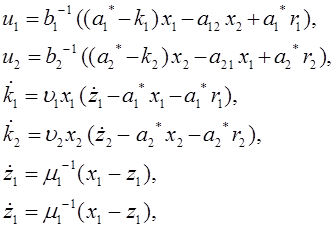 (4.8)
(4.8)
где ai* - коэффициенты эталонной модели. На
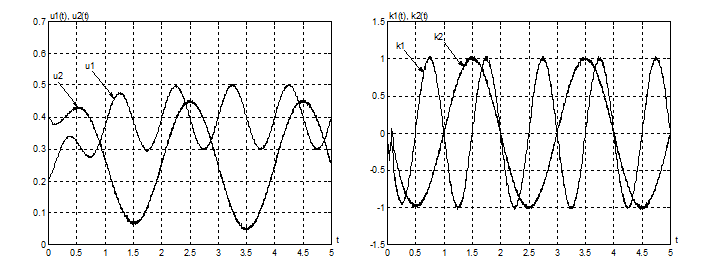
рис. 4.1, 4.2 показаны процессы, наблюдаемые в системе при постоянных входных
сигналах и следующих значениях параметров системы: ![]() ,
, ![]() ,
параметрические возмущения заданы вида
,
параметрические возмущения заданы вида ![]() .
Воздействие на вход системы импульсными сигналами приводит к процессам,
представленным на рис. 4.3 – 4.6. Нетрудно увидеть, что переходные процессы
удовлетворяют заданным показателям качества. При этом наблюдается ограниченное
по амплитуде управляющее воздействие в каждом канале. В начальный момент
времени отсутствуют «выбросы» выходных переменных регулятора, превышающих
среднее значение амплитуды колебаний. Разнотемповость движений хорошо заметна
на проекции фазового портрета в трехмерном пространстве (y1, y2, s1) (рис. 4.5). Из начальных условий
изображающая точка движется вдоль оси s1(
.
Воздействие на вход системы импульсными сигналами приводит к процессам,
представленным на рис. 4.3 – 4.6. Нетрудно увидеть, что переходные процессы
удовлетворяют заданным показателям качества. При этом наблюдается ограниченное
по амплитуде управляющее воздействие в каждом канале. В начальный момент
времени отсутствуют «выбросы» выходных переменных регулятора, превышающих
среднее значение амплитуды колебаний. Разнотемповость движений хорошо заметна
на проекции фазового портрета в трехмерном пространстве (y1, y2, s1) (рис. 4.5). Из начальных условий
изображающая точка движется вдоль оси s1(![]() ) при постоянных значениях y1, y2. Затем, начиная с некоторого момента
времени, когда s1 достигнет нулевого значения,
изображающая точка переходит на плоскость (y1,y2).
) при постоянных значениях y1, y2. Затем, начиная с некоторого момента
времени, когда s1 достигнет нулевого значения,
изображающая точка переходит на плоскость (y1,y2).
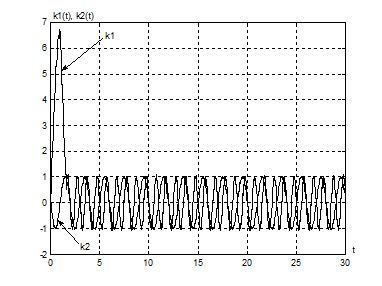
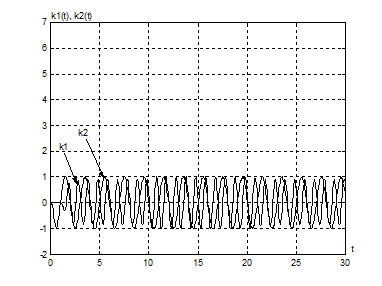
Влияние нелинейного звена
иллюстрируется на рис. 4.7, 4.8. Сравнение выходных процессов адапторов
позволяет говорить о том, что использование sgn(x) (рис. 4.7) приводит к увеличению амплитуды выходного
сигнала в течение первых двух секунд. Это обусловлено нулевым значением
входного воздействия по первому каналу. Так как ![]() , где
, где ![]() , то функция
, то функция ![]() остается
положительной и равной
остается
положительной и равной ![]() . Если производная
постоянна, то
. Если производная
постоянна, то ![]() , где
, где ![]() –
переменная времени. Следовательно,
–
переменная времени. Следовательно, ![]() является монотонно
возрастающей функцией.
является монотонно
возрастающей функцией.
Увеличение частоты и
(или) амплитуды параметрического возмущения приводит к необходимости увеличения
коэффициента передачи адаптора: ![]() , в частном случае,
когда параметры объекта изменяются по гармоническому закону, должно выполняться
неравенство:
, в частном случае,
когда параметры объекта изменяются по гармоническому закону, должно выполняться
неравенство: ![]() .
.
Замечание: Введение нелинейного звена с релейной характеристикой в адаптор позволяет добиться дополнительных «форсирующих» свойств при ненулевых начальных условиях в контуре настройки коэффициентов регулятора;
расчет параметров регулятора выполнен с учетом известных оценок темпа возмущений, что упрощает настройку адаптора;
алгоритмы адаптации (4.5), (4.7) можно получить на основе дифференциальной формы алгоритма скоростного градиента при соответствующем выборе функции цели;
желаемое качество выходных процессов обеспечивается при нулевых начальных условиях;
система сохраняет устойчивость независимо от ограниченных возмущений из заданного множества, координатных и параметрических начальных рассогласований в системе;
целесообразность использования рассмотренного класса адаптивных систем обусловлена жесткими требованиями к динамическим свойствам систем при существенной нестационарности характеристик объектов управления; также как в системах, рассмотренных в гл. 3 , качество работы в большей степени зависит от амплитуды и в меньшей степени – от частоты параметрических возмущений. Выбором коэффициентов передачи адаптора и блока желаемой динамики удается выполнить заданные требования по качеству переходных процессов.
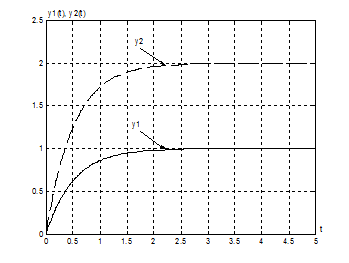
Рис. 4.1.

|
|
|
|
|
|
|
Рис. 4.5 |
Рис. 4.6 |

|
Рис. 4.7. |
Рис. 4.8 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.