Расчет одноканальной адаптивной системы. Модификации математической модели объекта управления. Синтез адаптивной системы полного порядка, страница 4

Алгоритмы настройки коэффициентов, синтезированные  по принципу локализации, могут быть двух видов (4.20), (4.21). Назовем   алгоритм адаптации (4.20) «гладким»,  а алгоритм     (4.21)–релейным. Сначала рассмотрим определение параметров «гладкого» алгоритма адаптации. Запишем уравнение системы с двумя контурами адаптации, подставив в него алгоритм управления:

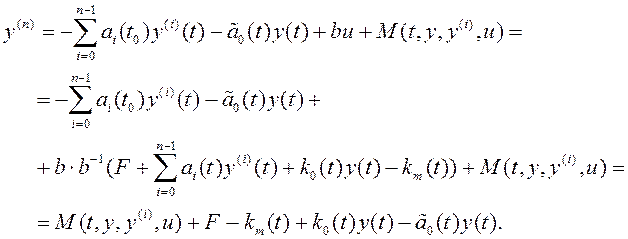         (4.34)

Учитывая введенные ранее обозначения, запишем уравнение связи между координатными и параметрическими рассогласованиями:

где  является отклонением настраиваемого параметра адаптивного регулятора  от неизвестного параметра объекта   Запишем модель  системы в отклонениях

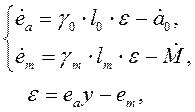                                                                      (4.35)

так как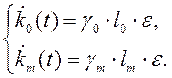 

Для проверки сходимости процессов  выберем функцию следующего вида:

которая является положительно определенной функцией, так как

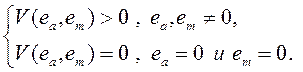
Полная производная выбранной функции равна

 .

Преобразуем полученное уравнение

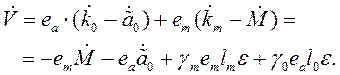                                                     (4.36)

Примем коэффициенты передачи адаптора равными между собой , тогда

                        

Для сходимости процессов необходимо выполнения условия

.

Оно будет справедливо, если    или . Это можно обеспечить соответствующим выбором  , например,  

                                                   .                                          (4.37)

Тогда производная исследуемой  функции будет иметь вид:

                                    

Из полученного выражения следует, что при ограниченных по модулю значениях отклонений для отрицательной определенности функции  и соответственно сходимости процессов   необходимо выполнение следующего условия:

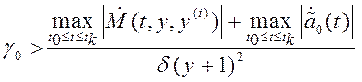                          ,                        (4.38)

где δ – допустимая динамическая ошибка,  0 < δ << ∞. Выражение (4.38) определяет оценку значений коэффициентов передачи адаптора. С учетом принятых допущений (4.37)  «гладкий» алгоритм адаптации имеет вид

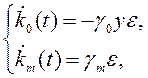
в котором значения коэффициентов  выбираются согласно выражению (4.38).

Перейдем к рассмотрению релейного алгоритма адаптации (4.21). Известно, что введение релейного элемента  повышает быстродействие адаптора. Представим алгоритм адаптации в следующем виде:

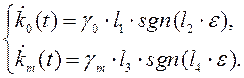                                                                        (4.39)

Задача состоит в определении  и функций l_i . Для ее решения также используем второй метод Ляпунова. Интуитивно понятно, что решение должно зависеть от вида исследуемой функции. Рассмотрим это подробнее. Сначала выберем функцию

производная которой  в силу уравнений системы (4.41) имеет вид:        

Пусть выполняется равенство тогда  

           

Как и в предыдущем случае примем , в результате чего имеем

                                   (4.40)

Потребуем выполнения равенства

оно достигается, если l_i  удовлетворяют условию

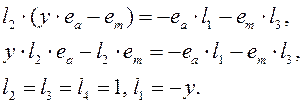                                                            (4.41) 

Подставим  l_i  из (4.41) в (4.39) и (4.40),  тогда релейный  алгоритм настройки коэффициентов запишется в виде

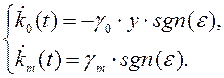                                                                            (4.42)         

а производная исследуемой функции -

Отсюда следует, что требование отрицательной определенности производной выбранной функции  выполняется, если коэффициенты передачи адаптора выбирать из условия (4.38).

Далее рассмотрим функцию в виде квадратичной формы относительно координатного рассогласования

                                                                                                    (4.43)

Производная данной функции с учетом выражения

и алгоритма адаптации (4.41) определяется следующим образом

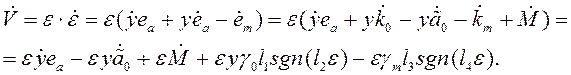
Для упрощения исследования примем  тогда

С помощью l_iобеспечим выполнение равенства  то есть