Расчет одноканальной адаптивной системы. Модификации математической модели объекта управления. Синтез адаптивной системы полного порядка, страница 2

  ,   (4.19)

здесь - настраиваемые коэффициенты, i={0, 1,…,n-1}.

Пусть коэффициенты регулятора образуют вектор , размерности -, тогда алгоритм адаптации со старшей производной запишется в виде

                                                                     (4.20)

или                                                 (4.21)

где – матрица коэффициентов передачи, ;– вспомогательные вектор-функции. Для сходимости процессов в системе (4.9), (4.19), (4.20)  элементы вектор-функции  определяются следующим образом [33]:

                                        (4.22)

где 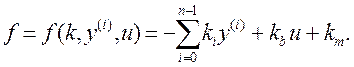 Таким образом, адаптивный регулятор описывается уравнениями

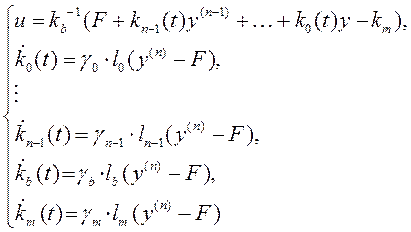                (4.23)

Согласно (4.22)  элементы  вектор-функции  имеют следующий вид:

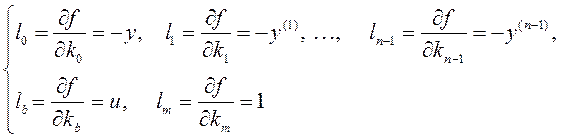
Для реализации синтезированного закона управления (4.23) требуется информация о производных выходной переменной, оценку которых можно получить с помощью линейной малоинерционной динамической  системы. Обычно такая система называется либо дифференцирующим фильтром, либо фильтром оценки производных (ФОП).  Дифференциальное уравнение ФОП имеет вид:

, где  - оценка . С учетом фильтра оценки производных порядок адаптивной системы  равен  где - число контуров настройки коэффициентов адаптивного регулятора,  , значение  зависит от количества неизвестных параметров и присутствия внешнего возмущения в  объекте управления.

4.2.3. Синтез адаптивной системы пониженного порядка

Сначала рассмотрим расчет адаптивной системы для объекта с модифицированной моделью 1-го вида  (4.13).

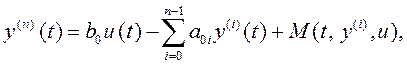
здесь , причем  равны либо расчетным номинальным значениям, либо априори известным верхним оценкам соответствующих коэффициентов. Таким образом, требуется парирование только аддитивного возмущения .

Следуя изложенной в п.4.2.2 последовательности расчета, закон управления в системе с одним контуром адаптации имеет вид:

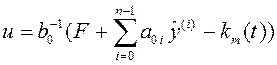                                      ,                           (4.24)

алгоритм сигнальной настройки:

                                      .                                  (4.25)

В данном случае порядок адаптивной системы с одним контуром адаптации равен  Структурная схема системы пониженного порядка с сигнальной адаптацией представлена на рис. 4.10. Нетрудно видеть, что полученная система может быть отнесена к классу робастных систем с астатическим регулятором (астатический регулятор со старшей производной). Таким образом, приведение модели линейного нестационарного объекта к виду (4.13) позволяет свести задачу синтеза адаптивного регулятора  к задаче синтеза астатического регулятора со старшей производной.

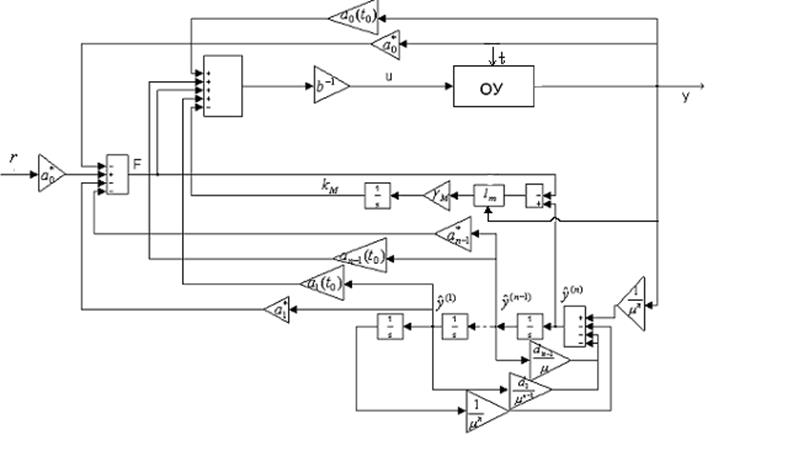
Рис. 4.10

Перейдем к рассмотрению модифицированной модели второго вида

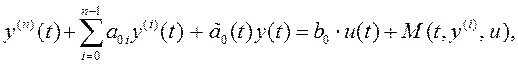                (4.26)

в которой помимо неизвестной функции M(t) присутствует неизвестный переменный параметр , т.е. на  объект действуют   параметрическое и аддитивное возмущения. Согласно последовательности синтеза адаптивной системы, в идеальный закон управления вводится два настраиваемых коэффициента

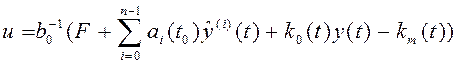,                 (4.27)

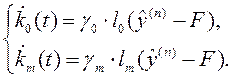                                                            (4.28)

Порядок адаптивной системы с двумя контурами адаптации равен  Структурная схема системы пониженного порядка с сигнально-параметрической адаптацией представлена на рис. 4.11.

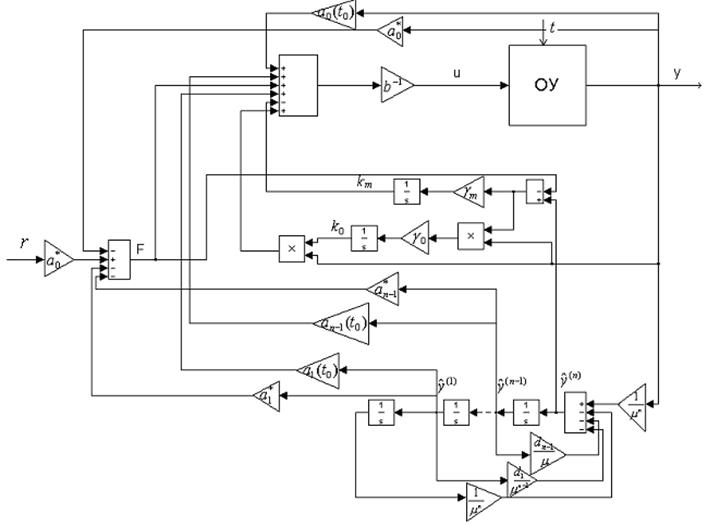
Рис. 4.11

4.2.4  Расчет параметров блока желаемой динамики

Вид переходных процессов в одноканальной стационарной системе зависит от расположения корней   характеристического многочлена. Поэтому формирование эталонного дифференциального уравнения связано с определением корней желаемого характеристического многочлена. Порядок желаемого дифференциального уравнения определяется порядком объекта управления (4.9). Поэтому выбираем n корней  , часть из которых может быть комплексно-сопряженными, и записываем желаемое характеристическое уравнение: