Расчет одноканальной адаптивной системы. Модификации математической модели объекта управления. Синтез адаптивной системы полного порядка, страница 3

или после раскрытия скобок                                    

                  (4.29)

Согласно (4.29) запишем однородное дифференциальное уравнение:

Так как цель управления заключается в стабилизации выходной переменной системы, то желаемое дифференциальное уравнение системы имеет вид:

.

4.2.5 Расчет параметров фильтра оценки производных

Реализация выбранного закона управления требует введение в систему фильтра оценки производных. Порядок фильтра определяется порядком старшей производной выходной переменной, которая используется в алгоритме настройки коэффициентов. С целью уменьшения влияния динамики фильтра оценки производных на свойства замкнутой системы его постоянная времени должна быть на порядок меньше минимальной постоянной времени блока желаемой динамики. Таким образом, процессы в фильтре должны быть значительно быстрее желаемых процессов на выходе системы. 

Так как необходимо оценивать n производных, то дифференциальное уравнение фильтра имеет вид:

где 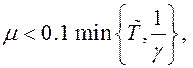    – оценка соответственно i-ой производной выходной переменной системы, коэффициенты  выбираются из условия устойчивости ФОП. Другой способ определения параметров ФОП состоит в выборе n корней характеристического полинома из допустимой области.  Границы этой области зависят от требуемых значений быстродействия (), перерегулирования () и статической ошибки (). По времени переходного процесса и статической ошибке находится корневая оценка степени устойчивости, 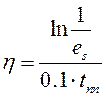   ,  а по перерегулированию – угол  между отрицательной вещественной полуосью и лучом, ограничивающим значения мнимой части корней, , .

4.2.6  Определение коэффициента передачи адаптора в системе с одним контуром настройки

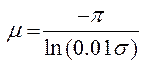Рассмотрим адаптивную систему с одним контуром адаптации вида (4.26). После определения коэффициентов блока желаемой динамики и параметров фильтра, необходимо найти значения коэффициента передачи адаптора. Последняя задача может быть решена с помощью второго метода Ляпунова.  Полагаем, что требуемые оценки производных координат состояний известны точно и  где – ограниченная рабочая область координат состояния.

Введем координатное и параметрическое рассогласования, а затем установим зависимость между. Пусть рассогласование между настаиваемым параметром регулятора  и структурно-параметрическим возмущением  оценивается по выражению

 , а отклонение траектории движения системы от желаемой  характеризуется переменной .

Подставим в уравнение объекта (4.13) закон управления (4.24). Полагая  и разрешив уравнение относительно старшей производной, получим:

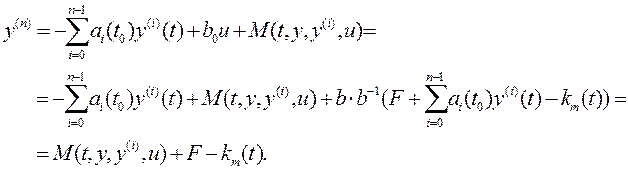          (4.30)

Тогда согласно введенным рассогласованиям и уравнению (4.30) следует справедливость выражения      ,    а полные производные по времени имеют вид  .                                    

Проверим сходимость  или  с помощью функции вида   которая является положительно определенной, так как

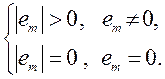
Полная производная рассматриваемой функции равна:

Подставим вместо  соответствующее выражение (4.25)

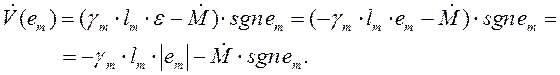         (4.31)

Пусть  вспомогательная функция алгоритма адаптации определяется согласно выражению

                                                   (4.32)

Следует отметить, что вид функции может быть  или , он определяется требованием отрицательной определенности .  Из условия простоты реализации адаптора  выбираем (4.32).  Коэффициент передачи адаптора должен удовлетворять неравенству

                                                                                          (4.33)

где  является ограничением темпа  изменения структурно-параметрического возмущения 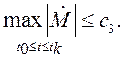 С учетом принятого допущения (4.32) адаптивный закон управления и алгоритм адаптации имеют следующий вид:

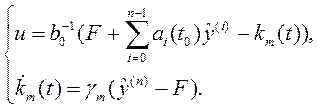
4.2.7. Определение параметров адаптора в системе с двумя контурами настройки