Синтез линейных импульсных систем. Постановка задачи синтеза. Наблюдатели состояния. Операторная процедура синтеза. Наблюдатели пониженного порядка. Основная идея

1.  Синтез линейных импульсных систем. Постановка задачи синтеза

Объект описывается системой разностных уравнений:

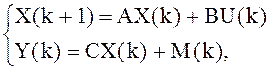
где M(k) - возмущение приложенное к выходу объекта, что при синтезе считается наиболее неблагоприятным случаем приложения возмущения.

Задача синтеза

1. После окончания переходного процесса выход объекта должен повторять входное задающее воздействие V:

.

В некоторых системах допускается наличие ошибки воспроизведения входного задающего значения:

.

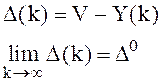2.Время переходного процесса должно быть не больше заданного: t_пп=t_з.

Рис. 1.1

3.Вид (качество) переходного процесса должен соответствовать заданному, часто задаётся величина перерегулирования 

Также необходимо проверить, управляем ли и наблюдаем ли объект.

2. Управляемость линейных импульсных систем

Запишем систему разностных уравнений, описывающих объект:

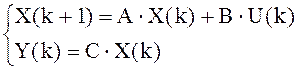
Рис. 1.2

Определение: объект управляем, если для любой пары начальных и конечных состояний существует конечное управляющее воздействие, которое на конечном интервале времени переводит объект из заданного начального состояния в заданное конечное, т.е. существует последовательность:

, пусть i=n-1

Рассмотрим задачу анализа управляемости одноканального объекта:

.

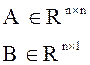Сформируем матрицу управляемости .

Критерий. Одноканальный объект управляем если матрица Г невырожденная. det Г¹0.

Доказательство. В соответствии с разностным уравнением объекта можно записать:

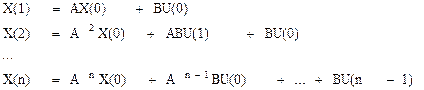
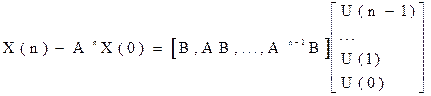
Таким образом последовательность управляющих воздействий переводящих объект из заданного начального состояния в заданное конечное находим следующим образом:

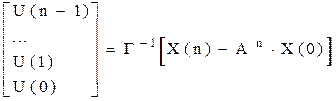, откуда и следует требование невырожденности Г.

1.1  3. Наблюдаемость линейных импульсных систем

Запишем разностные уравнения объекта:

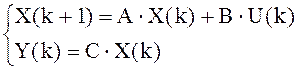
Пусть известно измеренное значение выхода и известна последовательность управляющих воздействий:

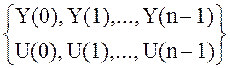, по этим данным необходимо найти X(k).

Определение. Объект наблюдаем, если по процессу Y(k) можно вычислить процесс X(k).

Матрицей наблюдаемости для одноканального объекта называется матрица вида:

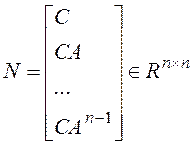, для одноканального объекта.

Критерий. Одноканальный объект наблюдаем, если матрица N невырожденная:

det N¹0.

Доказательство. Воспользуемся уравнением выхода:

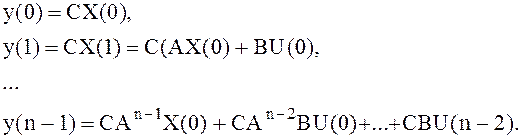
Здесь неизвестным является X(0), все остальные величины известны либо измеряемы. Запишем последние уравнения в матричной форме:

.

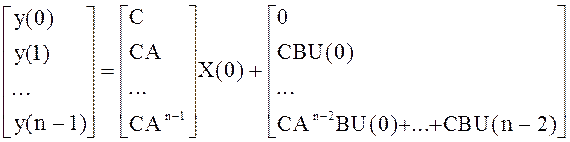Из последней системы уравнений выразим X(0):

.

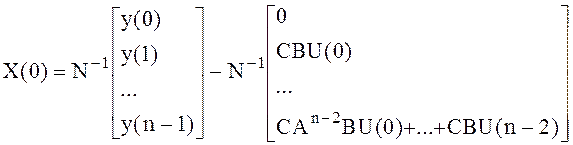Как видим, решение для X(0) существует только, если матрица N не вырожденная. Для оценки вектора состояния X(0) придется набирать информацию о выходе объекта за n шагов, начиная с нулевого.

1.1.1  4. Модальный метод синтеза. Астатическая процедура

Если необходимо обеспечить ошибку в системе равной нулю, то используется астатическая процедура синтеза.

Передаточная функция дискретного интегратора имеет вид:

,

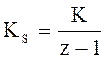K - свободный коэффициент.

Корректор динамики имеет передаточную функцию вида:

,

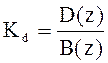dim D(z)=n-1,

,

 - свободные коэффициенты, подлежащие вычислению.

Выведем основные соотношения метода:

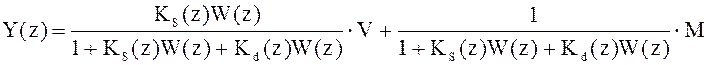
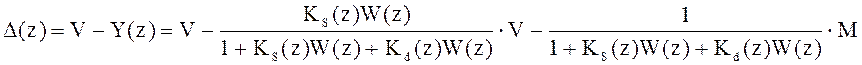
Подставим вместо K_s(z) его передаточную функцию:

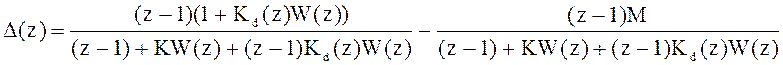
В статике k ® ¥, z ® 1 и, как видно из последнего равенства, ошибка в установившемся режиме будет равна нулю при любом входе и возмущении.

Рассмотрим характеристическое уравнение замкнутой системы:

,

,

.

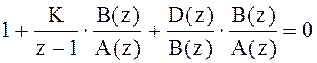Порядок характеристического уравнения системы равен (n+1), т.е. необходимо задать (n+1) желаемый корень. Для этого по желаемому виду переходного процесса найдем желаемую непрерывную передаточную функцию, а от неё посредством Z-преобразования перейдём к желаемой дискретной пердаточной функции:

,

,

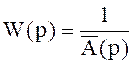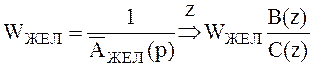
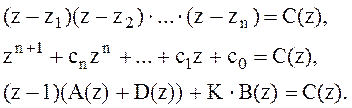
Последнее равенство и есть основное рабочее соотношение для нахождения искомых параметров корректоров статики и динамики.

Передаточную функцию объекта до начала синтеза следует обязательно отнормировать стандартным образом.

Приравнивая коэффициенты при одинаковых степенях z, получаем систему из (n+1) уравнения для нахождения  и K.

Отметим, что полный порядок системы с регулятором равен 2n, т.к. порядок объекта  - n, порядок корректора динамики - (n -1), порядок корректора статики равен 1.

1.1.2  5. Модальный метод синтеза. Статическая процедура модального метода синтеза

Структура системы остается без изменений.

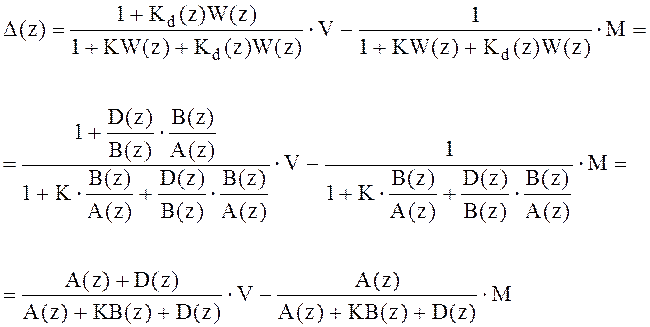
Знаменатель данного выражения - характеристический полином всей системы (порядок его n).

Искомыми параметрами являются  и K.

A(z)+D(z)+KB(z)=C(z),

,

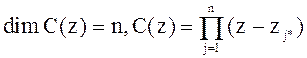При синтезе задается величина ошибки, либо абсолютное значение при заданных пределах изменения входа и возмущения, либо в процентах от входного воздействия. Систему уравнений для нахождения искомых параметров регулятора необходимо дополнить уравнением статической ошибки, при этом получим (n+1) уравнение для поиска (n+1) искомого параметра регулятора:

1.2  6. Матричная процедура модального метода синтеза

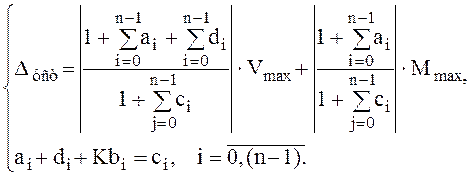
Пусть задана модель объекта в форме Коши, а управление формируется в виде обратных связей по состоянию объекта:

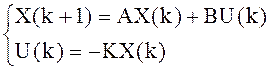
Будем считать, что вектор состояния полностью измерим.

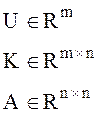
Подставим управление в уравнения объекта:

X(k+1)=AX(k)+B(-KX(k))

X(k+1)=(A-BK)X(k)

Из последнего уравнения формируем характеристический полином и приравниваем его желаемому:

det[zI-A+BK]=(z).

Матрица K содержит больше неизвестных коэффициентов, чем уравнений порождаемых последним равенством, поэтому часть коэффициентов можно задать произвольно, часто их задают нулевыми, но n штук должны остаться свободными.

Рекомендация: при выборе коэффициентов  матрицы K (n штук) надо, чтобы в каждый коэффициент при степенях z правой части последнего равенства вошел хотя бы один из свободных коэффициентов.