Синтез линейных импульсных систем. Постановка задачи синтеза. Наблюдатели состояния. Операторная процедура синтеза. Наблюдатели пониженного порядка. Основная идея, страница 2

1.2.1  7. Матричная процедура модального метода синтеза. Применение для одноканального объекта

Модель объекта:

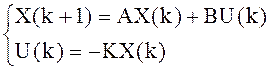
Отличие от предыдущей процедуры только в размерностях:

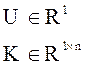
Матрица K представляет собой матрицу строку.

Процедура синтеза значительно облегчается, если модель объекта представить в «прямой» форме Коши:

;                       ;

;                 ;

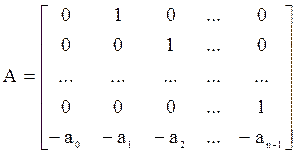Полагаем, что коэффициенты матриц А, В, С порождены передаточной функцией:

.

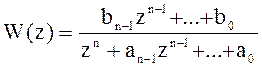Запишем уравнения замкнутой системы:

X(k+1)=(A-BK)X(k),

тогда матрица правой части вычисляется следующим образом:

.

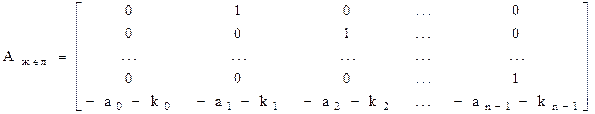В характеристическое уравнение войдут только коэффициенты из последней строки этой матрицы, тогда система уравнений для нахождения коэффициентов матрицы K выглядит так:

,             , где с_i коэффициенты желаемого характеристического полинома.

1.3  8. Синтез одноканальных астатических систем с использованием матричной процедуры

Модель объекта:

.

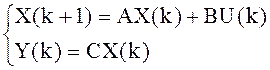Рис. 3.3

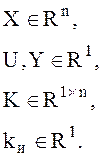
Рассмотрим процедуру синтеза на примере объекта третьего порядка:

;                               

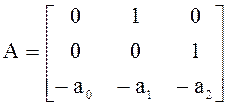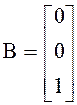
Расширим модель объекта, добавив разностное уравнение интегратора:

.

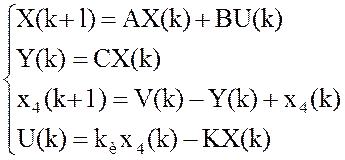Полная система уравнений объекта с регулятором приведена ниже:

.

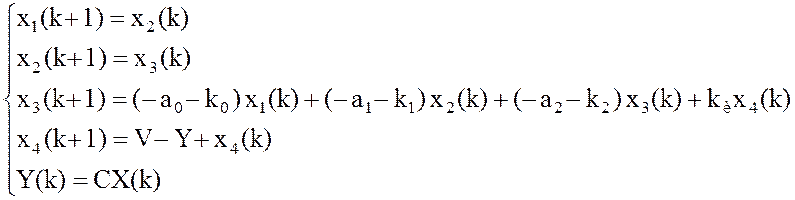Матрица  полной системы выглядит следующим образом:

.

Приравняв характеристический полином всей системы желаемому характеристическому полиному, составленному из желаемых корней, а далее приравняв коэффициенты этих полиномов при равных степенях оператора z, получаем систему уравнений для нахождения параметров регулятора, она приведена ниже в матричной форме. Матрицы хорошо структурированы и методом математической индукции полученный результат может быть распространен на системы любого порядка.

               

На примере системы третьего порядка видно, что система уравнений для поиска параметров регулятора хорошо структурирована. Для любого порядка методом математической индукции можно записать матрицу левой части и вектор правой части этого уравнения.

Ограничение операторной процедуры модального метода синтеза:

операторную процедуру можно применять для объектов, у которых корни числителя (нули) лежат в круге единичного радиуса. Для матричной процедуры модального метода синтеза такого ограничения нет.

Для реализации матричной процедуры модального метода синтеза необходимо иметь полную информацию о векторе состояния, либо иметь оценку вектора состояния.

9. Наблюдатели состояния. Операторная процедура синтеза.

1.4  Одноканальный случай

Рассмотрим структуру наблюдателя Люинбергера:

Рис. 0.1

Y и  будут совпадать только при совпадении параметров объекта и модели и при одинаковых начальных условиях объекта и модели, если не ввести звено обратной связи в наблюдателе.

L(z) - звено обратной связи в наблюдателе.

С помощью L(z) можно свести D к нулю и сделать это нужно как можно быстрее.

;      

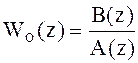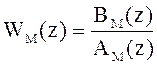
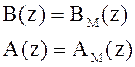
Это однородное разностное уравнение, в случае его устойчивости положение равновесия по D будет 0.

Преобразуем последнее выражение:

A(z)D(z)+L(z)B(z) D(z)=0,

(A(z)+L(z)B(z)) D(z)=0,

Получено характеристическое уравнение наблюдателя, его корни должны быть заданными для того, чтобы обеспечить требуемые динамические свойства наблюдателя.

Пример 1. Наблюдатель для объекта первого порядка.

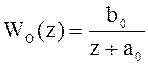
Потребуем, чтобы процессы в контуре имели минимальную длительность.

,

.

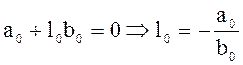Пример 2. Наблюдатель для объекта второго порядка.

Пока корректор L(z) нереализуемый.

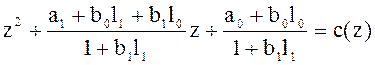
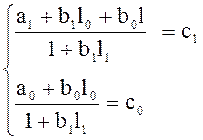
Потребуем, чтобы процессы в контуре имели минимальную длительность.

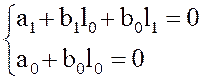
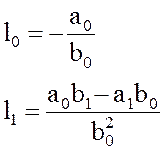
пример 3 (рабочий)

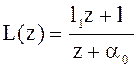
Наблюдатель получается (2n-1) порядка.