Синтез линейных импульсных систем. Постановка задачи синтеза. Наблюдатели состояния. Операторная процедура синтеза. Наблюдатели пониженного порядка. Основная идея, страница 3

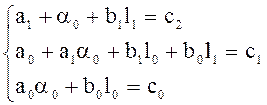
или в векторно-матричной форме:

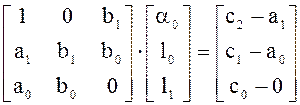
пример 4

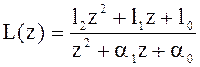
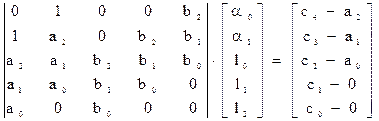
Выводы:

Порядок корректора L(z) для таких наблюдателей равен (n-1).

Порядок наблюдателя в целом (2n-1).

Минимальное время переходного процесса не более (2n-1) шагов.

При небольших отклонениях параметров наблюдателя и объекта данный наблюдатель можно использовать для оценки вектора состояния объекта.

1.5  10. Матричные наблюдатели состояния (многоканальные)

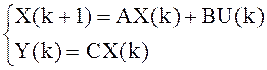
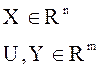
До того, как строить наблюдатель надо проверить наблюдаемость объекта.

Рис. 0.2

Как видно из структурной схемы, данный наблюдатель позволяет получить оценку вектора состояния , кроме того он позволяет получить прогноз вектора состояния , а с его помощью можно получить прогноз выхода (умножив на матрицу C).

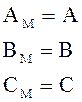
Введём новую переменную:

X(k+1)=AX(k)+BU(k)

Уравнение получилось однородным. Если наблюдатель устойчив, то e(k) стремится к нулю и, при  этом,  стремится к X.

Наблюдатель имеет тот же порядок, что и объект.

Характеристическое уравнение наблюдателя имеет вид:

Пример 1.Набдюдатель для объекта второго порядка.

;           ;      ;       

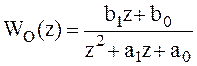
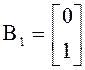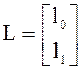
Характеристическое уравнение наблюдателя имеет вид:

.

Потребуем, чтобы в наблюдателе были процессы минимальной длительности, тогда:

.

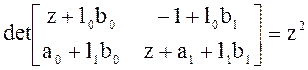Уравнения для вычисления параметров наблюдателя получим следующие:

.

1.6  11. Синтез матричных наблюдателей для одноканальных объектов

Для облегчения расчетов модель объекта удобно представить в «транспонированной» форме Коши:

;                       ;     ;        .

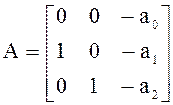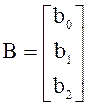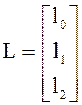Характеристическое уравнение наблюдателя имеет вид:

det(zI-A+LC)=C_Ж

,

.

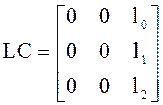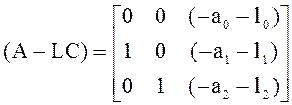Параметры матрицы L вычисляются в указанном базисе очень просто:

.

1.7  12. Переход от одного базиса к другому

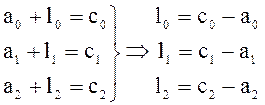В некоторых задачах для удобства расчета бывает необходимо перейти от исходного базиса, в котором записаны уравнения объекта, к другому базису. Рассмотрим эту процедуру перехода, где Т – матрица преобразования базисов, X₁ – новый базис.

X₁=TX              X=T^-1X₁

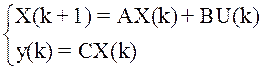
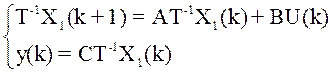
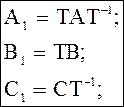
пример 1

A₁T=TA

A₁                                                                                                         A

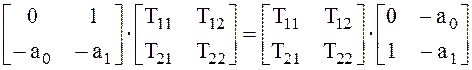
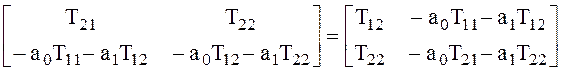
Эта система получилась недоопределённая, т.к. второе и третье уравнения в ней совпадают (T₁₂= T₂₁), а четвертое уравнение - тождество.

Воспользуемся уравнением преобразования матриц В:

В        В₁

,

,

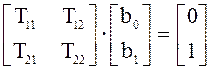
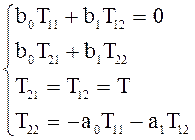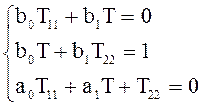В итоге получим в матричной форме следующее решение:

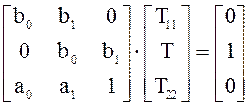
Пример 2

13. Наблюдатели пониженного порядка. Основная идея

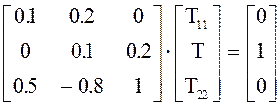
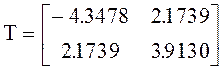
Математическая модель объекта задается в форме Коши:

        

    

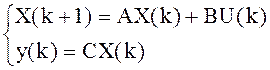
X_Н - наблюдаемая часть вектора состояния,

X_И - измеряемая часть вектора состояния,

Перейдём к новому вектору состояния, в котором в качестве измеряемой компоненты используется вектор выхода y:

,   ,    

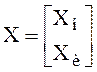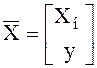
Преобразуем исходную модель объекта:

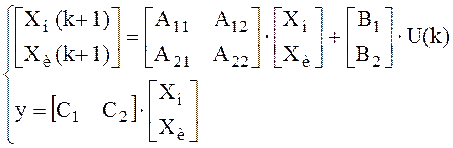
Найдем матрицу связи между старым и новым базисом:

Легко показать, используя уравнения выхода, что клетки матрицы T  имеют следующий вид:

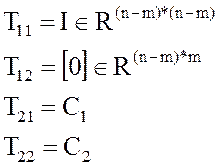, а матрица .

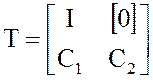Уравнения объекта в новом базисе принимают вид:

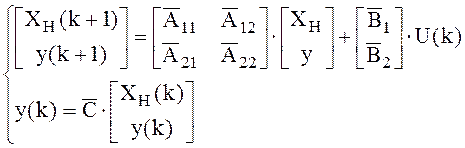
Матрицы объекта в новом базисе вычисляются по обычной процедуре:

,             ,                   .

1.7.1  Уравнения наблюдателя

Уравнения объекта в новом базисе имеют вид:

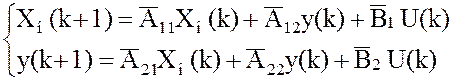
Уравнения наблюдателя:

Выражение для невязки примем без доказательства:

Подставим невязку в систему уравнений:

14. Наблюдатели пониженного порядка. Структурная схема.

1.7.2   

 

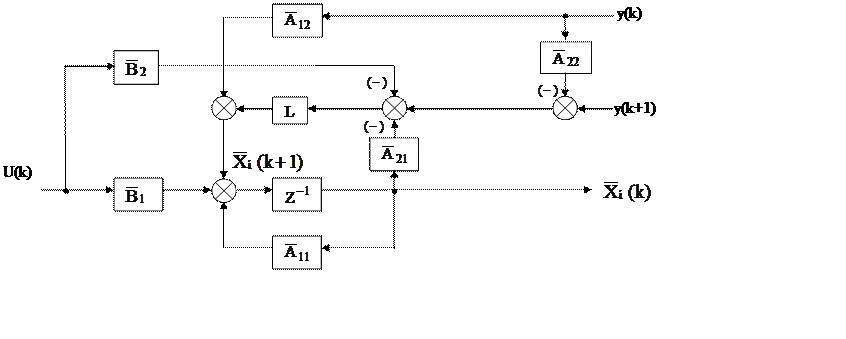Рис. 4.3

Простыми структурными преобразованиями удается избавиться от y(k+1):

 

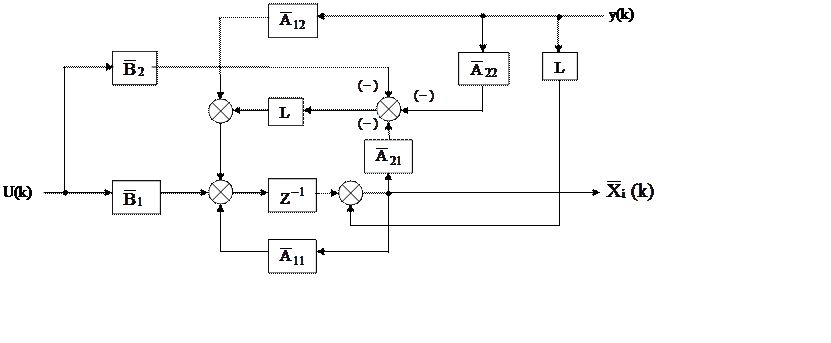Рис. 4.4

Но теперь в этой схеме нет прогноза вектора X(k+1) и быть не может.

1.8  15. Особенности динамики систем с наблюдателями

Запишем полную систему уравнений, описывающую объект управления с регулятором и наблюдателем:

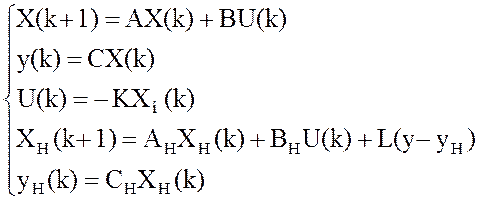
Предполагаем