Введем новую переменную:
![]()
![]()
![]()
Перепишем исходную систему уравнений, используя новую переменную:
 .
.
Приведем подобные в последнем выражении:
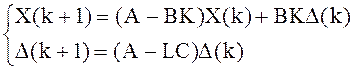 .
.
Перепишем это выражение в матричном виде:
 .
.
Матрица правой части получилась треугольная. Запишем характеристическое уравнение полученной системы:
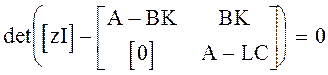
Известно, что определитель для треугольной квадратной матрицы имеет следующий вид:
det(zI-A+BK)×det(zI-A+LC)=0, т.е. собственные числа этой матрицы представляют собой две группы, первая из которых - это группа желаемых корней синтезируемой системы, вторая группа корней - это группа желаемых корней наблюдателя, используемого для оценки вектора состояния объекта.
Динамика полной системы с наблюдателем и регулятором описывается двумя независимыми наборами корней:
желаемые корни системы реализуются с помощью матрицы K;
желаемый набор корней наблюдателя состояния реализуется с помощью матрицы обратных связей L.
Оба набора корней формируются независимо друг от друга, следовательно, динамические свойства фильтра и объекта взаимно друг на друга не влияют, но процессы по выходу объекта, до тех пор пока не закончатся переходные процессы в наблюдателе, зависят от последних.
Наблюдатель - неуправляемая подсистема.
(Пропорциональный - интегральный - дифференцирующий)
|
Структурная схема системы с ПИД-регулятором приведена на рисунке.
Рис. 2.1
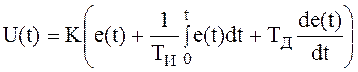
Существуют специальные процедуры параметрического синтеза для нахождения параметров.
|
Рис. 2.2
Добавка ![]() позволяет увеличить запас устойчивости по
фазе.
позволяет увеличить запас устойчивости по
фазе.
Воспользуемся приближенной процедурой интегрирования по методу прямоугольников и первой разностью для реализации процедуры дифференцирования:
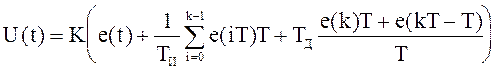
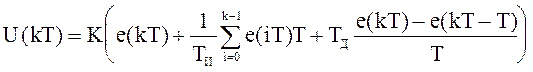 .
.
С точки зрения цифровой реализации удобнее не прямой алгоритм, а рекуррентный, поэтому найдем управление на предыдущем шаге, затем разность между текущим управлением и предыдущим и с помощью этой разности построим рекуррентную процедуру вычисления управления:
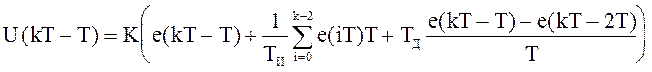
D(kT)=U(kT)-U(kT-T)ÞU(kT)=U(k)
U(k)=U(k-1)+D(k)
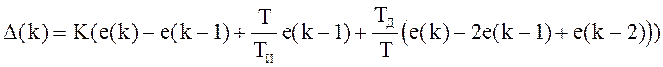

![]() - это и есть искомый алгоритм.
- это и есть искомый алгоритм.
Представим его в операторной форме:
![]()
![]()
Найдем передаточную функцию цифрового ПИД-регулятора:
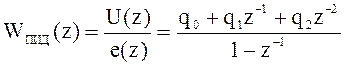

На рисунке приведенном ниже представлена структурная интерпретация цифрового ПИД-регулятора.
|
Рис. 2.3
Первая модификация связана с использованием более точной процедуры интегрирования по методу трапеций:
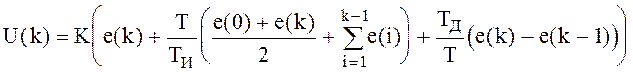 ,
,
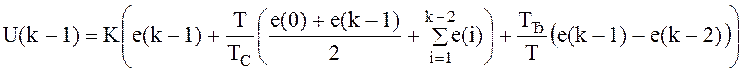 ,
,

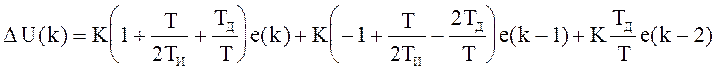
![]()
Итоговое выражение для управления не изменилось, но изменились выражения для вычисления коэффициентов qi.
Цель - уменьшить рывки в управляющем воздействии. Исключаем для этого в дифференцирующей компоненте входное задающее воздействие:
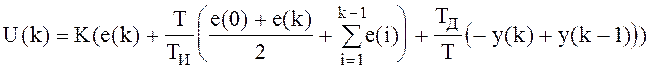
![]()
Цель та же - уменьшить рывки в управляющем воздействии. Считаем, что входное воздействие изменяется достаточно медленно, поэтому его можно исключить и из пропорциональной компоненты управления:
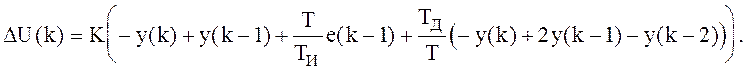
Маленькая модификация связана со сдвигом аргумента в интегрирующей компоненте на шаг вперед, это увеличивает запас устойчивости системы:
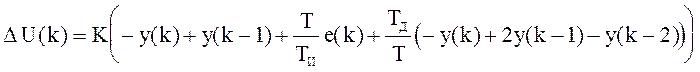 .
.
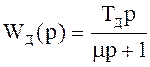
|
Рис. 2.4
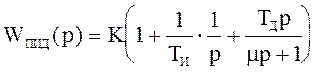
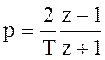 Преобразования Тастина
Преобразования Тастина
![]()
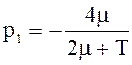
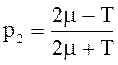
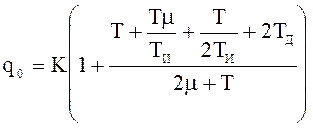
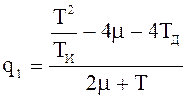
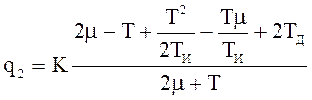
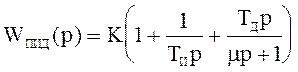

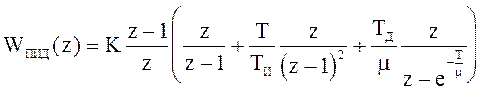
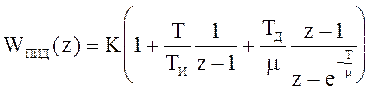
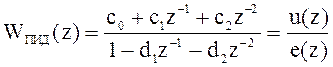
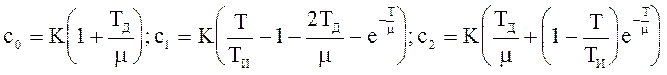
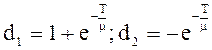
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.