Министерство образования и науки Российской Федерации
Новосибирский Государственный Технический Университет
Лабораторная работа №2
АНАЛИЗ СВОЙСТВ СИСТЕМЫ ПОИСКА ЭКСТРЕМУМА
СО СТАРШЕЙ ПРОИЗВОДНОЙ В УПРАВЛЕНИИ
Факультет: АВТ
Группа: АА-86
Студенты: Сапрыкин О.Н. Преподаватель:
Лядов А.Д. Французова Г.А.
Вариант: 2
г. Новосибирск
2012
Цель работы: Исследовать свойства градиентной системы поиска экстремума, основанной на методе локализации. Оценить влияние дифференцирующего фильтра и фильтра оценки частной производной на характер переходных процессов.
Исходные данные:
|
параметры |
k0 |
Т |
а |
tn |
|
значения |
3 |
2 |
1 |
5 |
Функциональная схема:
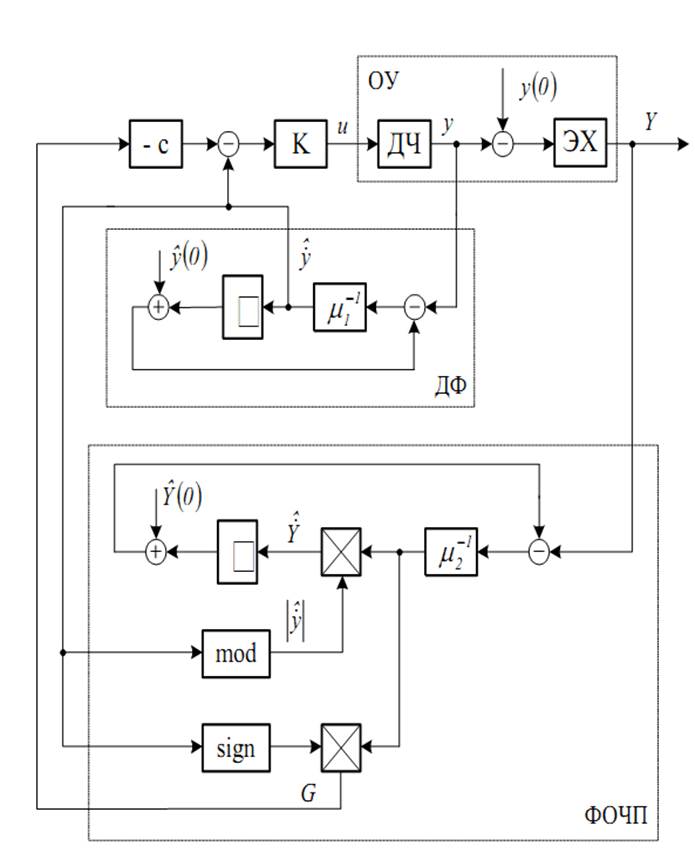
Рис. 1. Структурная схема системы поиска экстремума
Результаты эксперимента:
3.1 Определить параметры регулятора и фильтров на основании требований к качеству работы системы
![]()
![]()
![]()
3.2. Собрать модель замкнутой системы и зарисовать
переходные процессы y(t), Y(t)
и G(t), задавая начальные условия ![]() , а
, а ![]() . Рассмотреть траекторию движения
системы на плоскости (y, Y)
. Рассмотреть траекторию движения
системы на плоскости (y, Y)
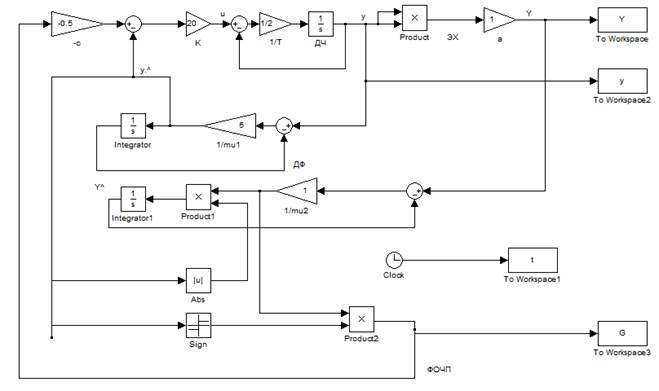
Рис. 2. Модель замкнутной системы
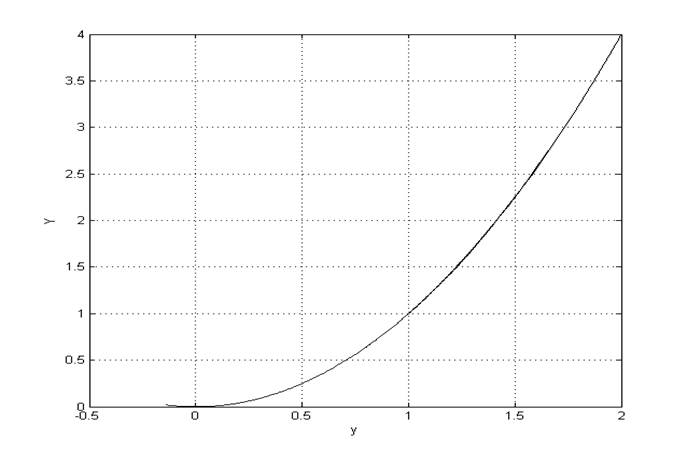
Рис.3. Траектория движения системы в координатах (y, Y)
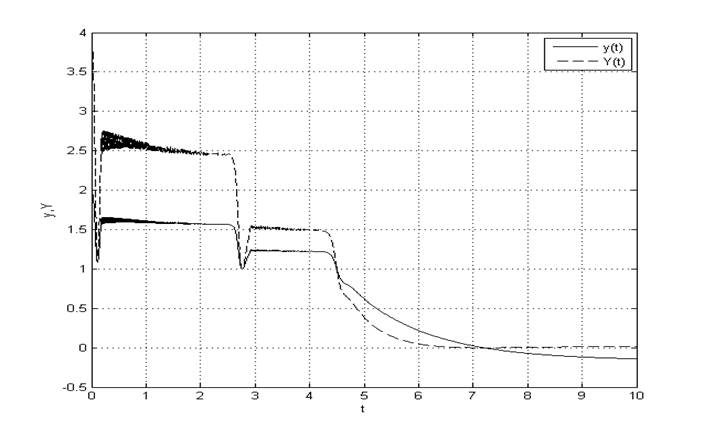
Рис. 4. Переходные процессы y(t), Y(t) при начальных условиях
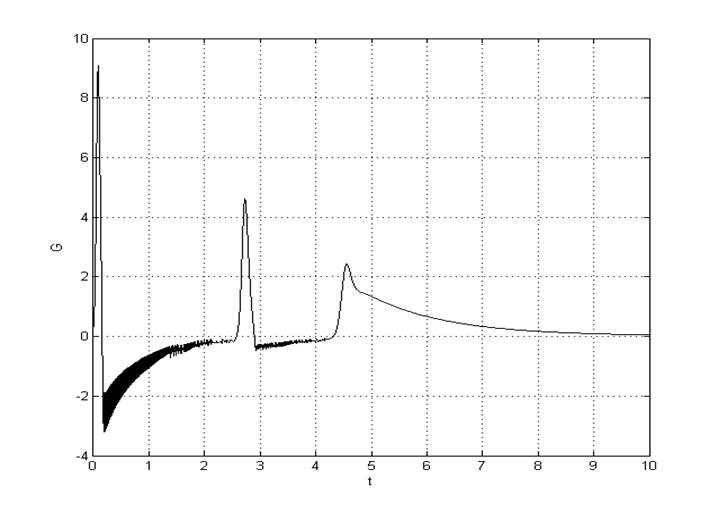
Рис. 5. Переходный процесс G(t) при начальных условиях
3.3 При ![]() исследовать влияние начальных
условий ФОЧП на y(t), Y(t) и G(t), изменяя
исследовать влияние начальных
условий ФОЧП на y(t), Y(t) и G(t), изменяя ![]() в диапазоне (0,6÷5)
в диапазоне (0,6÷5)![]()
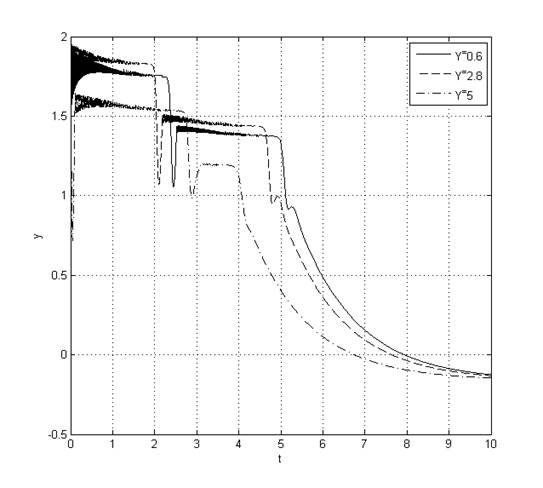
Рис. 6. Переходный процесс y(t) при ![]()
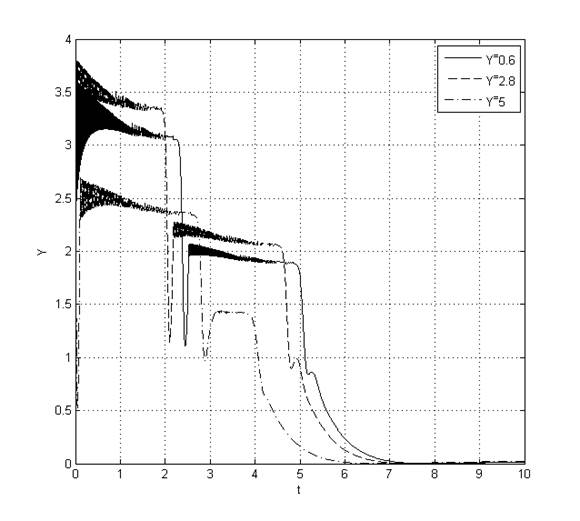
Рис. 7. Переходный процесс Y(t) при ![]()
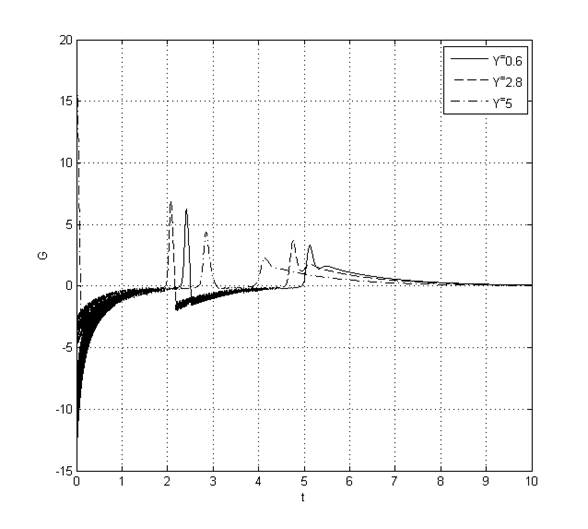
Рис. 8. Переходный процесс G(t) при ![]()
3.4 Исследовать влияние параметра с на характер процессов, уменьшая и увеличивая его значение в 5 раз при исходных значениях начальных условий ДФ и ФОЧП. Сравнить результаты с процессами, полученными в п.4.1. Зарисовать переходные процессы y(t), Y(t) и G(t).
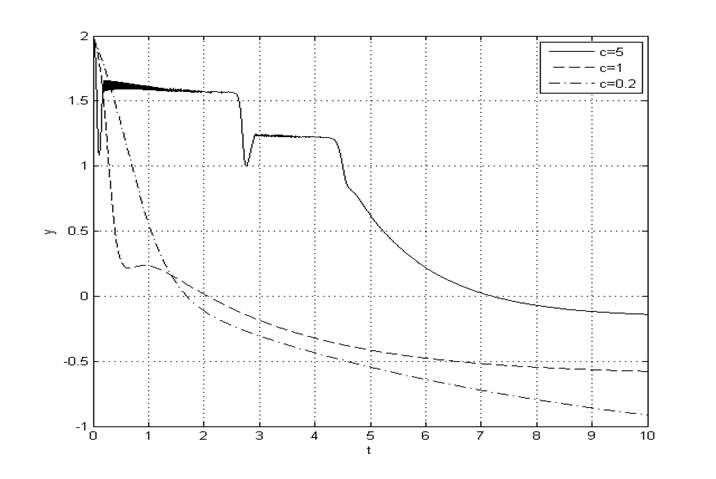
Рис. 9. Переходный процесс y(t) при ![]()
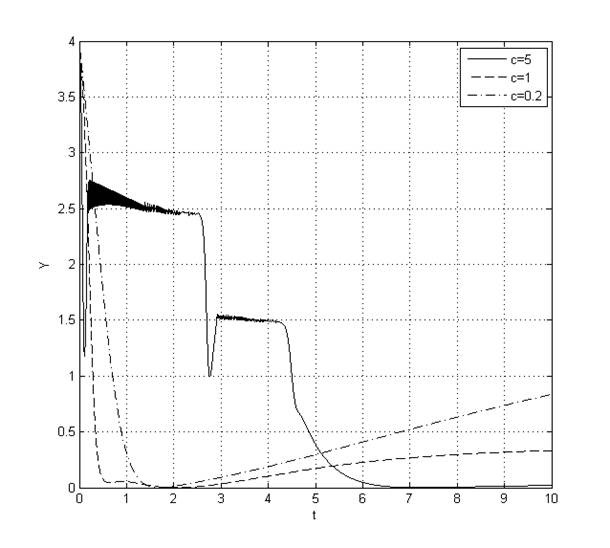
Рис. 10. Переходный процесс Y(t) при ![]()
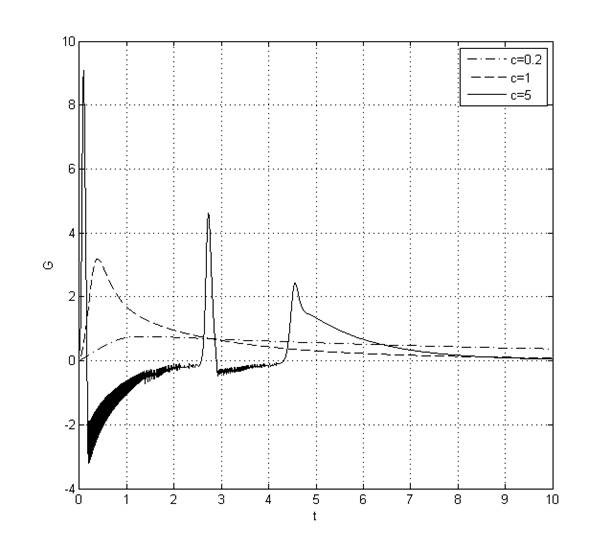
Рис. 11. Переходный процесс G(t) при ![]()
3.5 При ![]() и
и ![]() оценить влияние параметра
оценить влияние параметра ![]() на процессы в системе, уменьшая
его значение в 5 раз относительно
на процессы в системе, уменьшая
его значение в 5 раз относительно ![]()
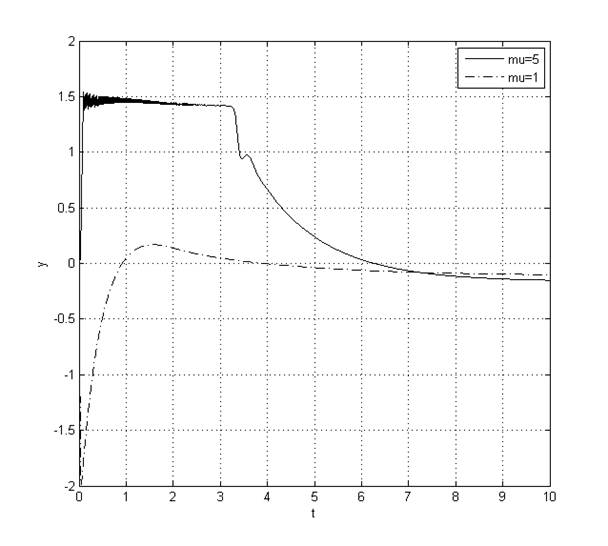
Рис. 12. Переходный процесс y(t) при ![]()
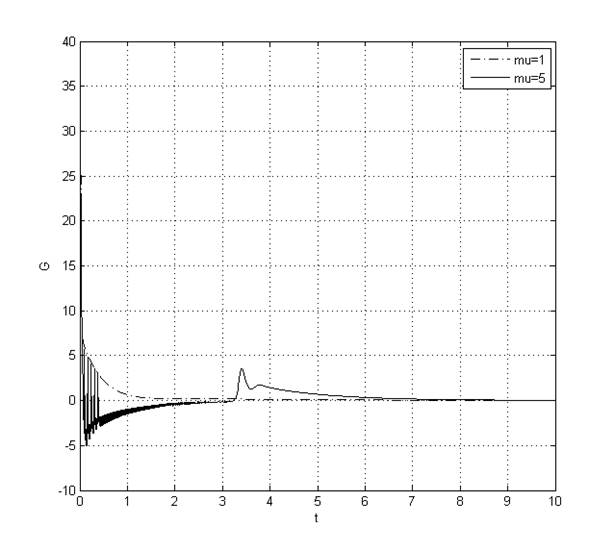
Рис. 13. Переходный процесс G(t) при ![]()
3.6 При ![]() и
и ![]() проанализировать влияние параметра
проанализировать влияние параметра
![]() на процессы в системе, уменьшая
его значение в 5 раз относительно рассчитанного значения
на процессы в системе, уменьшая
его значение в 5 раз относительно рассчитанного значения
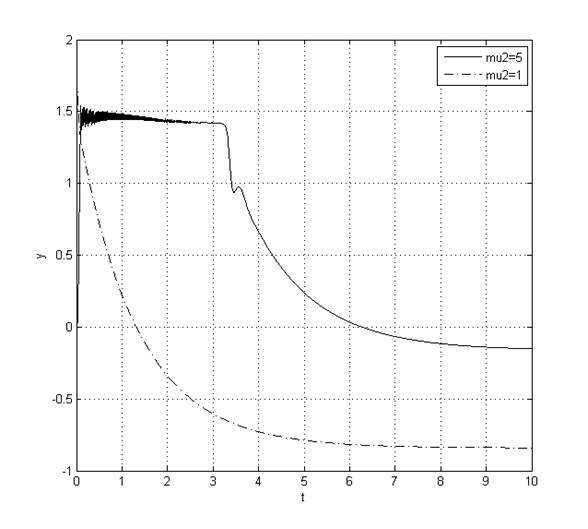
Рис. 14. Переходный процесс y(t) при ![]()
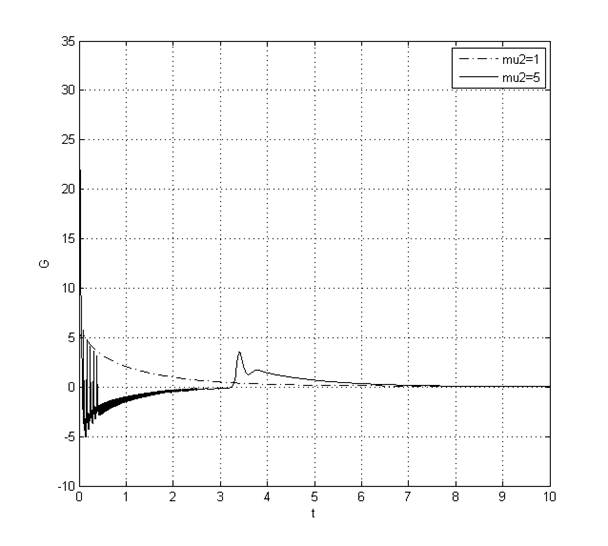
Рис. 15. Переходный процесс G(t) при ![]()
Выводы:
В ходе лабораторной работы были исследованы градиентной системы поиска экстремума, основанной на методе локализации. Проведена оценка влияния параметров системы на характер переходных процессов.
Изменение ![]() в малом диапазоне значений
практически не влияет на качества переходных процессов в системе, однако, при
значительном изменении этого параметра значение оценки градиента резко
увеличивается, что делает задачу поиска экстремума неразрешимой.
в малом диапазоне значений
практически не влияет на качества переходных процессов в системе, однако, при
значительном изменении этого параметра значение оценки градиента резко
увеличивается, что делает задачу поиска экстремума неразрешимой.
При уменьшении коэффициента с увеличивается время переходного процесса, но переходный процесс становится более "гладким" и наоборот. При значительном увеличении этого параметра задача поиска экстремума также становится неразрешимой.
Уменьшение ![]() приводит к увеличению времени
переходных процессов в системе.
приводит к увеличению времени
переходных процессов в системе.
Уменьшение ![]() приводит к уменьшению времени
переходных процессов в системе, но значительно уменьшается точность найденного
значения экстремума.
приводит к уменьшению времени
переходных процессов в системе, но значительно уменьшается точность найденного
значения экстремума.
Влияние параметра с на переходные процессы y(t) и Y(t) взаимно пропорционально
Увеличение с приводит к увеличению броска в начальный момент переходного процесса G(t), поэтому увеличить с в 5 раз не удалось.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.