Исследование свойств оптимальной по быстродействию системы

МИНЕСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра Автоматики

Лабораторная работа №3

Исследование свойств оптимальной по быстродействию системы

Факультет: АВТ

Группа: ААМ-10

Студент:                                                                               Преподаватель:

Солдаткин А.                                                                                   Французова Г.А.  

Дата выполнения:

Отметка о защите:

Новосибирск, 2010

Цель работы: знакомство с принципом построения оптимальных и субоптимальных систем, анализом влияния основных параметров на ее переходные процессы и фазовый портрет.

Исходные данные:

Задан объект управления, модель которого имеет вид

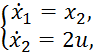
Требуется обеспечить в замкнутой системе оптимальные по быстродействию процессы перехода из произвольного начального состояния  в заданное конечное, которое совпадает с началом координат, т.е. .

Расчет оптимального закона управления:

Формируется оптимальный закон управления в виде

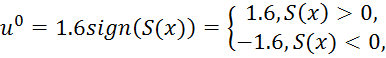
где  – линия переключения управляющего воздействия, которая описывается уравнением

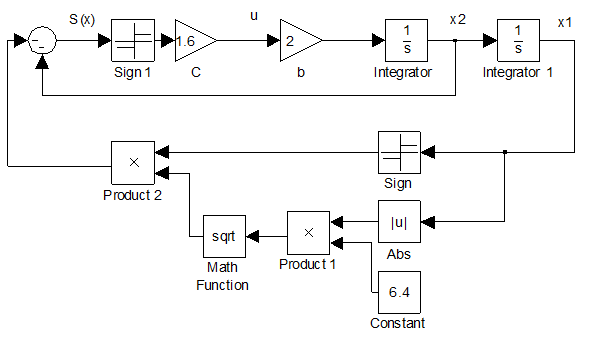
Рис. 1. Структурная схема оптимальной системы

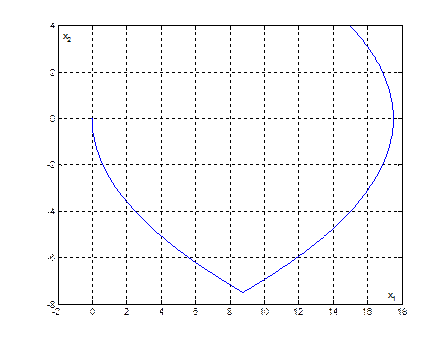
Рис. 2. Фазовая траектория из начальной точки

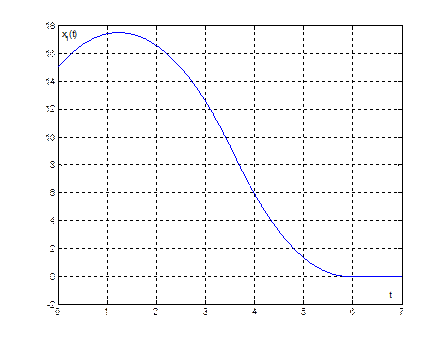
Рис. 3. График переходного процесса

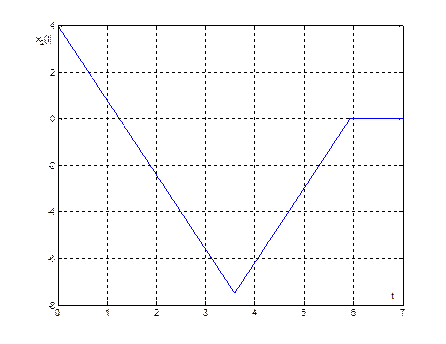
Рис. 4. График переходного процесса

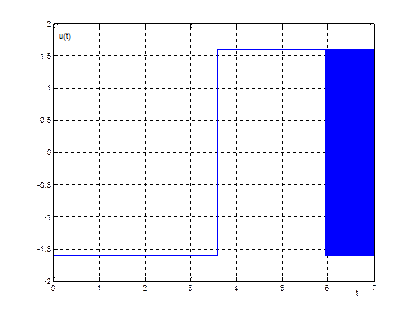
Рис. 5. График переходного процесса

Время переходного процесса

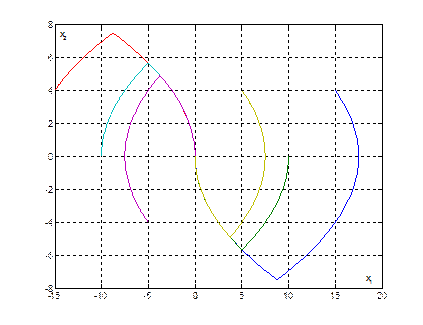
Рис. 6. Фазовый портрет системы

Исследуем влияние  на оптимальные процессы , , , задавая , .

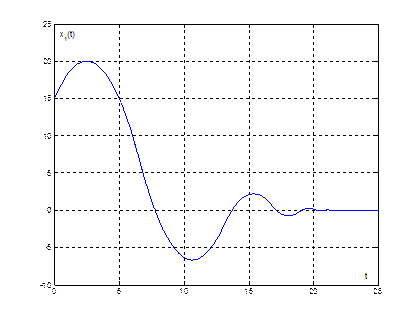
Рис. 7. График переходного процесса  при

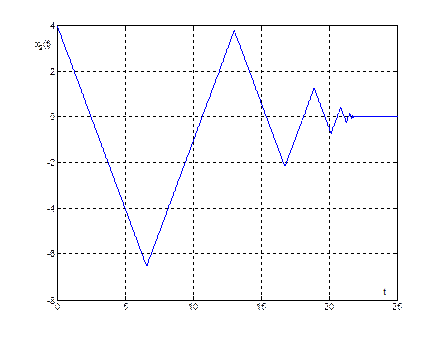
Рис. 8. График переходного процесса  при

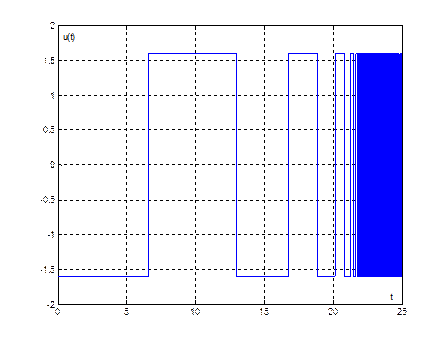
Рис. 9. График переходного процесса  при

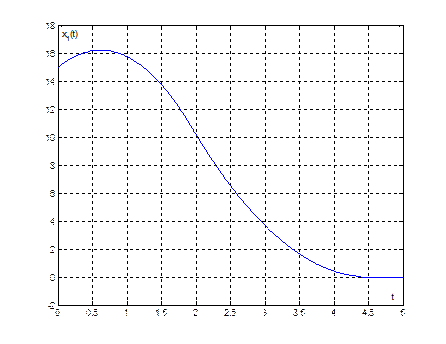
Рис. 10. График переходного процесса  при

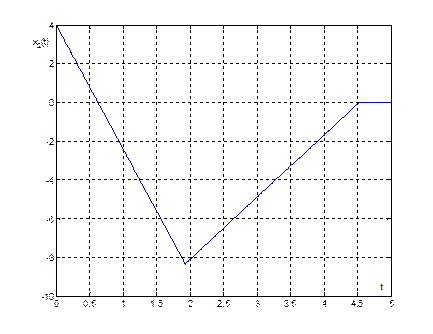
Рис. 11. График переходного процесса  при

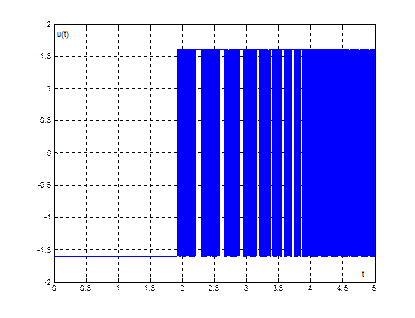
Рис. 12. График переходного процесса  при

Исследуем влияние уровня ограничения управляющего воздействия  на оптимальные процессы , , , задавая .

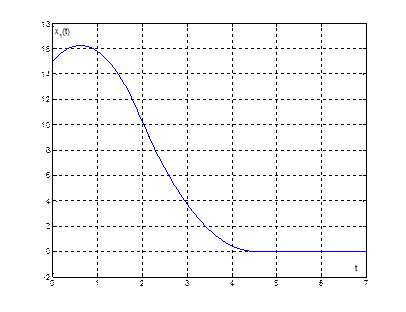
Рис. 13. График переходного процесса  при

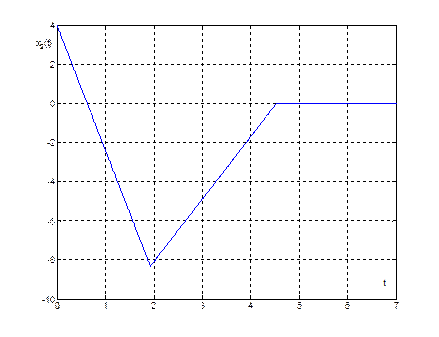
Рис. 14. График переходного процесса  при

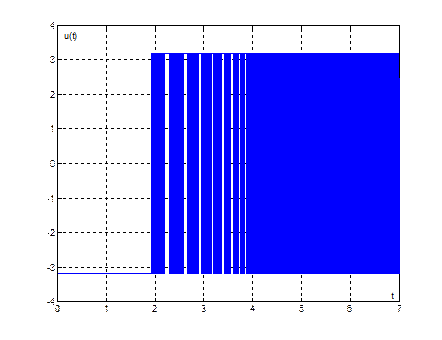
Рис. 15. График переходного процесса  при

Аппроксимируем линию переключений прямой, пересекающей линию переключения в точках (-15, 9.8) и (15, -9.8):

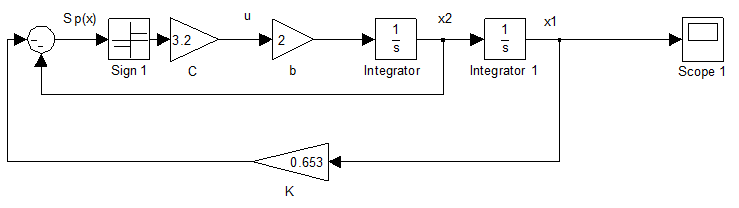
Рис. 16. Структурная схема субоптимальной системы

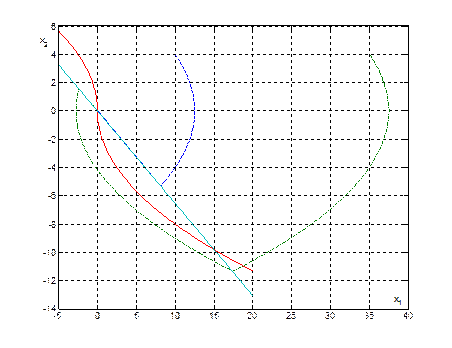
Рис. 17. Фазовые траектории субоптимальной системы при различных начальных условиях.

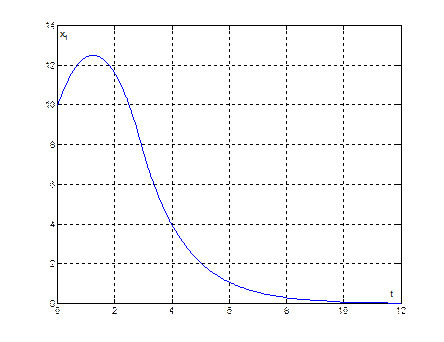
Рис. 18. График переходного процесса , при начальных условиях (10,4)

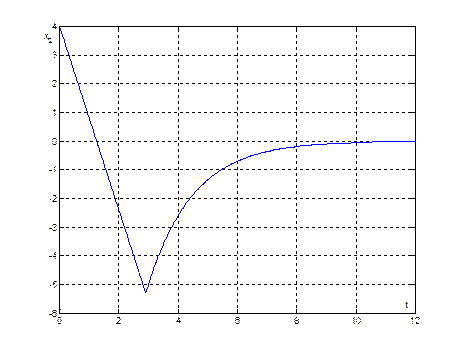
Рис. 19. График переходного процесса , при начальных условиях (10,4)

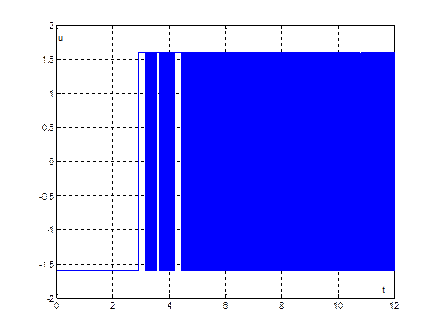
Рис. 20. График переходного процесса , при начальных условиях (10,4)

Длительность переходного процесса из начальных условий (10,4) .

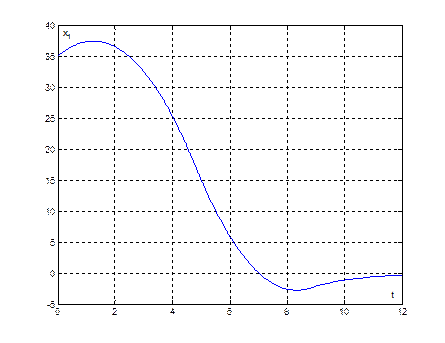
Рис. 21. График переходного процесса , при начальных условиях (35,4)

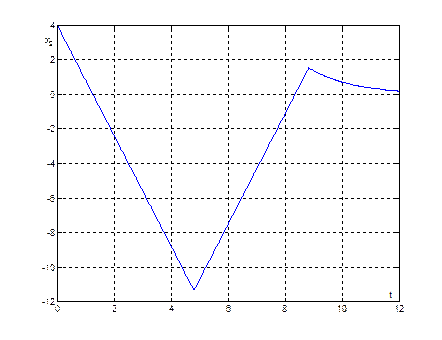
Рис. 22. График переходного процесса , при начальных условиях (35,4)

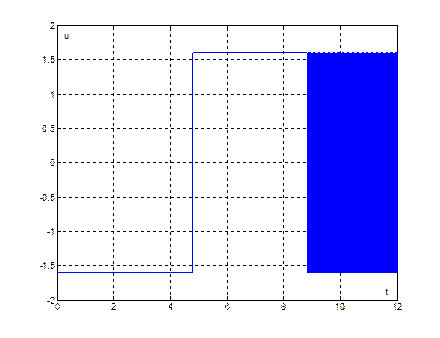
Рис. 23. График переходного процесса , при начальных условиях (35,4)

Длительность переходного процесса из начальных условий (35,4) .

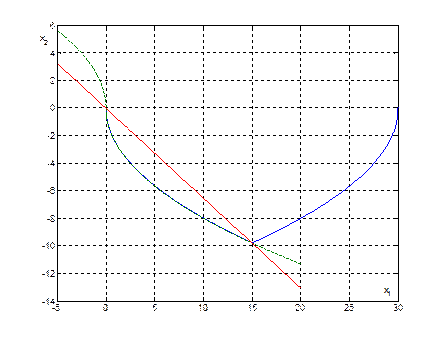
Рис. 24. Фазовая траектория субоптимальной системы при начальных условиях (30,0).

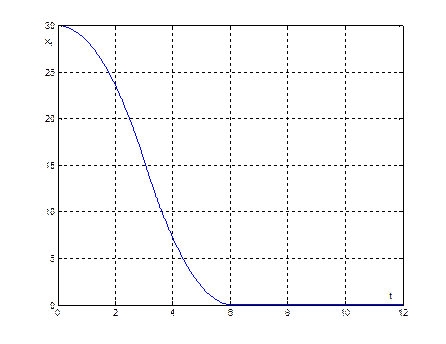
Рис. 25. График переходного процесса , при начальных условиях (30,0)

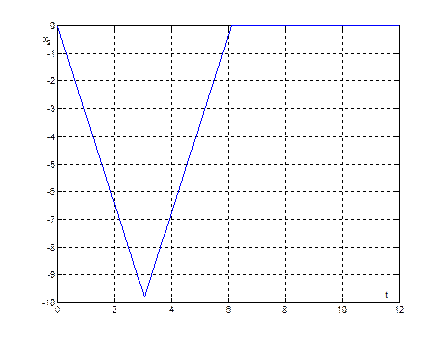
Рис. 26. График переходного процесса , при начальных условиях (30,0)

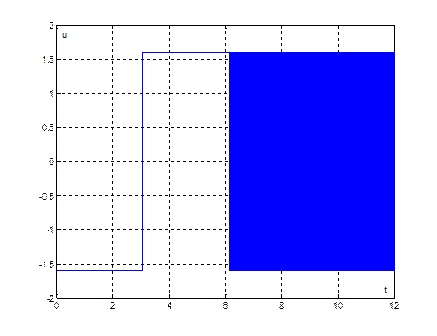
Рис. 27. График переходного процесса , при начальных условиях (30,0)

Длительность переходного процесса из начальных условий (30,0) .

Исследуем влияние  на субоптимальные процессы, задавая .

Аппроксимируем линию переключений прямой, пересекающей линию переключения в точках (-4.9, 3.75) и (4.9, -3.75):

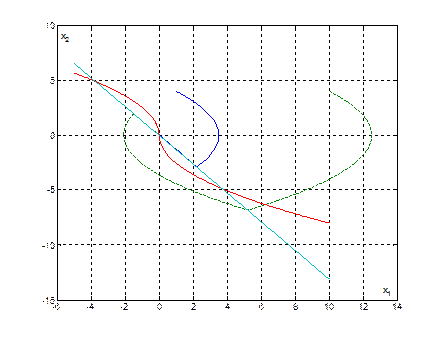
Рис. 28. Фазовые траектории субоптимальной системы при различных начальных условиях.

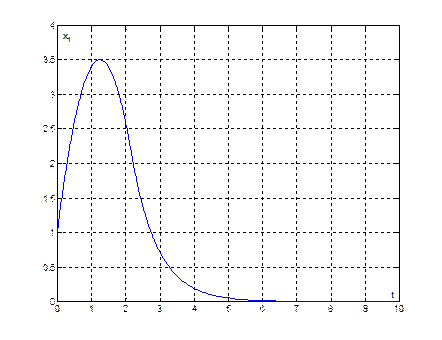
Рис. 29. График переходного процесса , при начальных условиях (1,4)

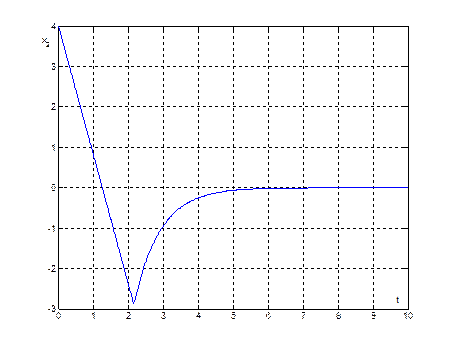
Рис. 30. График переходного процесса , при начальных условиях (1,4)

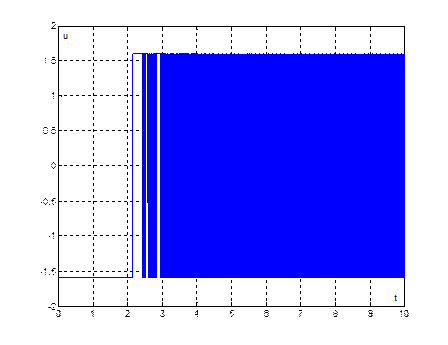
Рис. 31. График переходного процесса , при начальных условиях (1,4)

Длительность переходного процесса из начальных условий (1,4) .

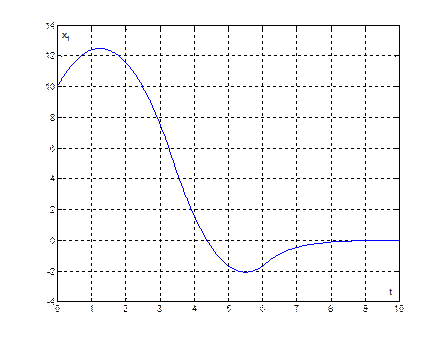
Рис. 32. График переходного процесса , при начальных условиях (10,4)

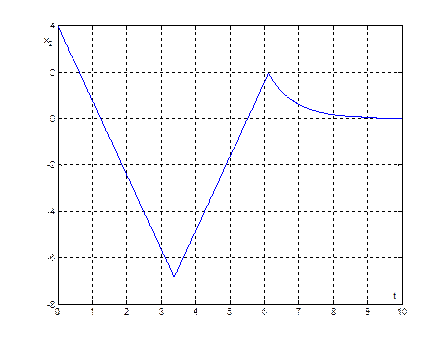
Рис. 33. График переходного процесса , при начальных условиях (10,4)

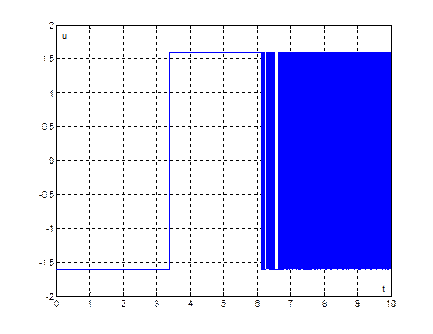
Рис. 34. График переходного процесса , при начальных условиях (10,4)

Длительность переходного процесса из начальных условий (10,4) .

Вывод:

В ходе работы была разработана и исследована оптимальная система управления.

При переводе объекта из точки (15, 4) в начало координат происходит одно переключение управляющего воздействия, что согласуется с теоремой о числе переключений (по теореме в такой системе может быть не больше одного переключения).

При изменении коэффициента усиления объекта система движется не по оптимальным траекториям. При увеличении коэффициента усиления переход в конечную точку осуществляется за меньшее время, но не за минимально возможное для такого значения коэффициента.

Увеличение максимального значения управления так же приводит к уменьшению времени перехода в конечную точку, но это время является так же не оптимальным.

Субоптимальная система была получена путем аппроксимации поверхности переключения прямой, проходящей через заданные точки. В субоптимальной системе возникает скользящий режим.

Процессы в субоптимальной системе будут существенно зависеть от начальных условий. Так, при движении из точки (10,4) изображающая точка системы попадает на реальную линию переключений, а затем движется вдоль нее в скользящем режиме. Из начальной точки (35,4) изображающая точка системы будет доходить до реальной линии переключений, переключаться на траекторию, соответствующую другому знаку управления, вновь попадает на реальную линию переключений и двигается вдоль нее в скользящем режиме. Из начальных условий (30,0) изображающая точка системы будет попадать в точку пересечения идеальной и реальной линий переключения и к началу координат будет двигаться по оптимальной траектории.