Анализ свойств системы поиска экстремума со старшей производной в управлении

МИНЕСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра Автоматики

Лабораторная работа №2

Анализ свойств системы поиска экстремума со старшей производной в управлении

Факультет: АВТ

Группа: ААМ-10

Студент:                                                                               Преподаватель:

Солдаткин А.А.                                                                               Французова Г.А.  

Дата выполнения:

Отметка о защите:

Новосибирск 2010

Цель работы: исследовать свойства градиентной системы поиска экстремума, основанной на методе локализации. Оценить влияние дифференцирующего фильтра и фильтра оценки частной производной на характер переходных процессов.

Исходные данные:

Задан объект управления, который описывается уравнениями

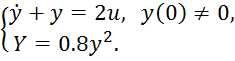
Желаемое время выход на экстремум .

Расчет параметров системы поиска экстремума:

На основании требований к длительности переходного процесса выхода на экстремум формируется желаемое уравнение:

С учетом градиента, который для заданного объекта равен , желаемое уравнение записывается в форме

Согласно методу синтеза формируется управляющее воздействие

где  – коэффициент усиления регулятора, численное значение которого выбирается из диапазона

Примем .

Для реализации закона управления используется дифференцирующий фильтр. При отсутствии помехи измерения используется фильтр 1-го порядка со следующей моделью

где  и  являются оценками  и  соответственно;  – постоянная времени дифференцирующего фильтра.

Оценка градиента  (частной производной в данном случае) осуществляется с помощью специального фильтра, модель которого имеет вид

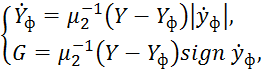
где  – постоянная времени фильтра оценки частной производной (ФОЧП).

Выполнение работы:

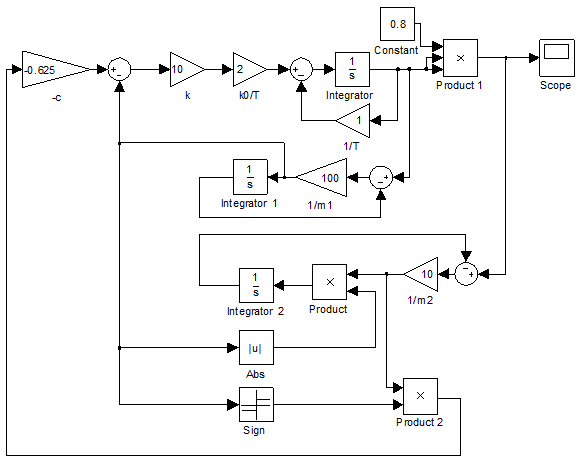
Рис. 1. Структурная схема системы поиска экстремума со старшей производной в управлении

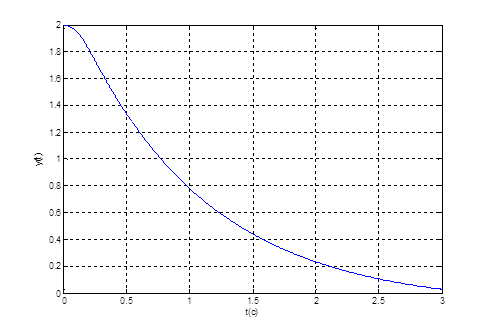
Рис. 2. График переходного процесса  при  и .

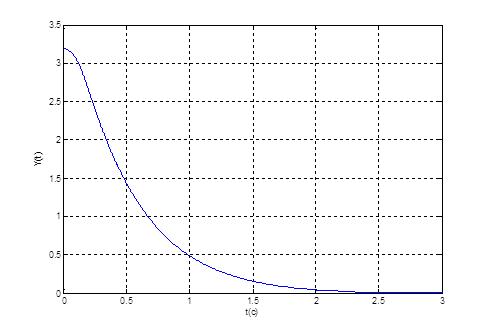
Рис. 3. График переходного процесса  при  и .

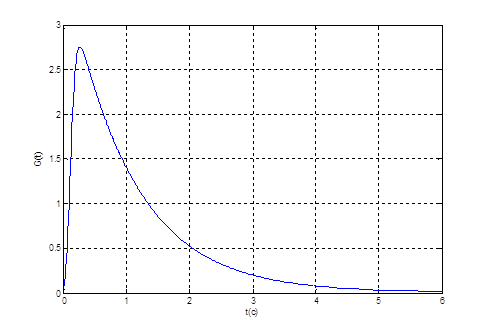
Рис. 4. График переходного процесса  при  и .

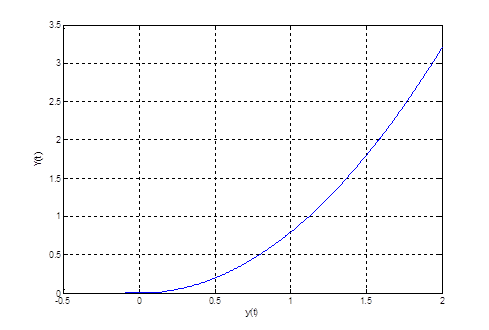
Рис. 5. Портрет системы на плоскости  при  и .

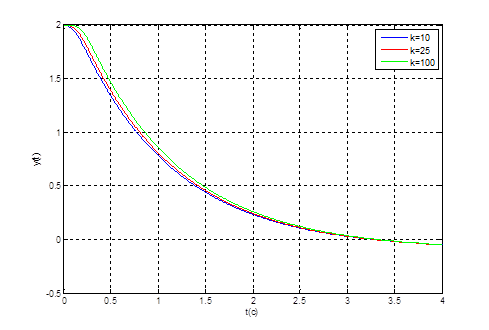
Рис. 6. Графики переходных процессов  при   и при  и

 

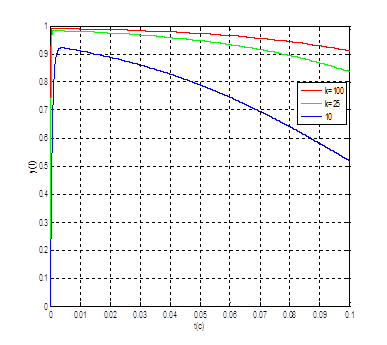
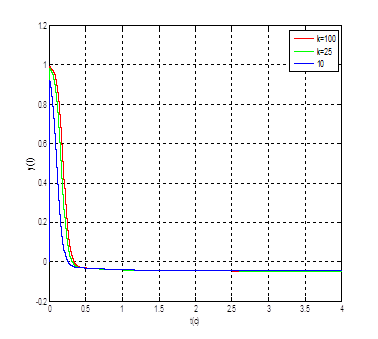
Рис. 7. Графики переходных процессов  при   и при  и

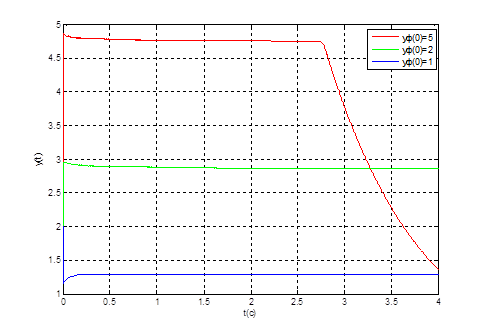
Рис. 8. Графики переходных процессов при ,  и

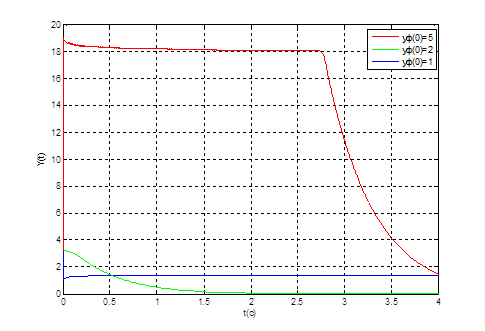
Рис.9. Графики переходных процессов при ,  и

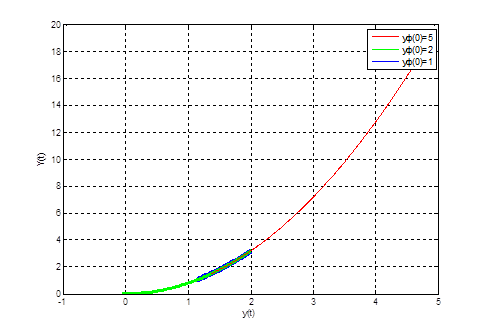
Рис. 10. Портрет системы на плоскости  при ,  и

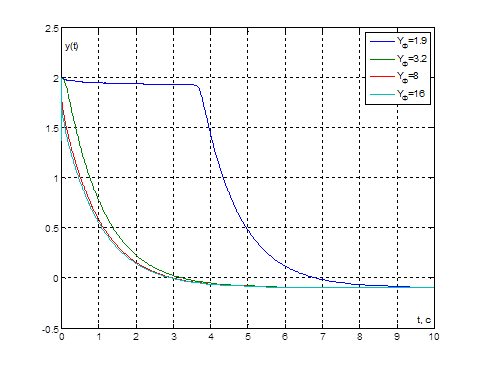
Рис. 11. Графики переходных процессов при  и

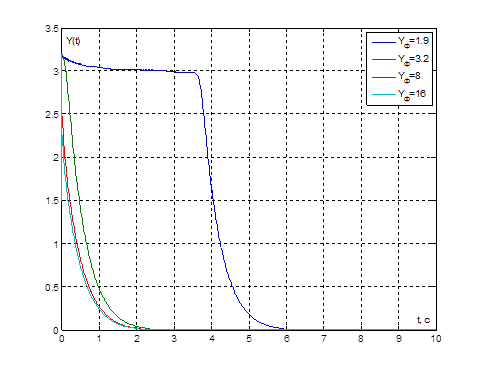
Рис. 12. Графики переходных процессов при  и

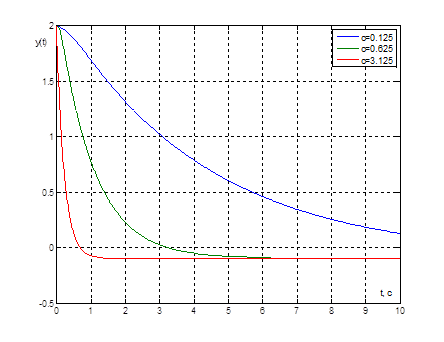
Рис. 13. Графики переходных процессов при  и и при значениях параметра

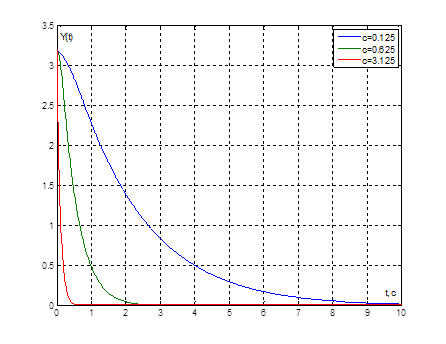
Рис. 14. Графики переходных процессов при  и и при значениях параметра

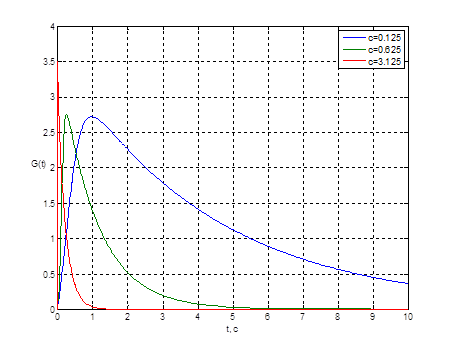
Рис. 15. Графики переходных процессов при  и и при значениях параметра

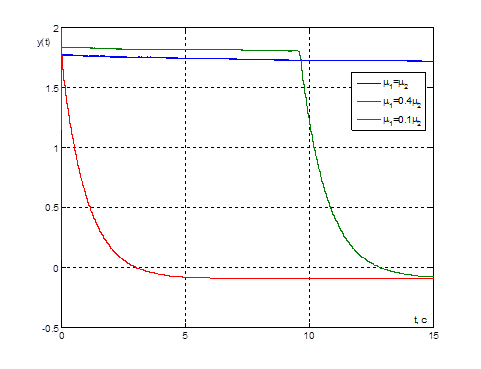
Рис. 16. Графики переходных процессов при  и и при значениях параметра

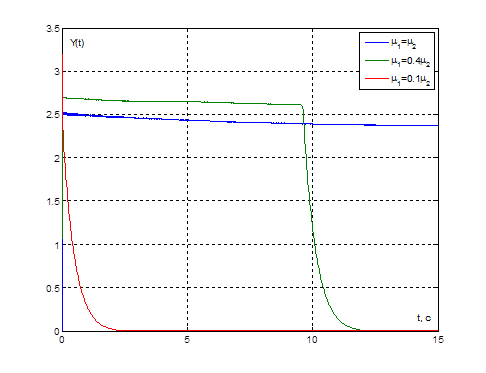
Рис. 17. Графики переходных процессов при  и и при значениях параметра

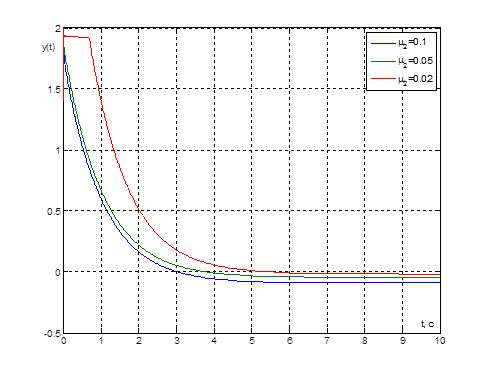
Рис. 18. Графики переходных процессов при  и и при значениях параметра

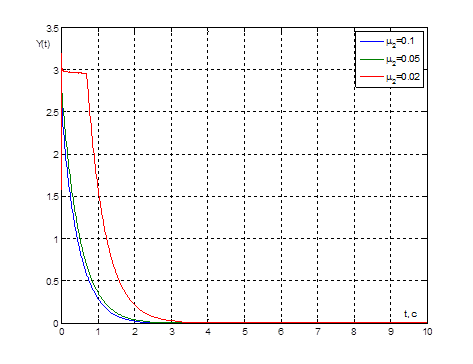
Рис. 19. Графики переходных процессов при  и и при значениях параметра