Машиностроение \ Теория машин и механизмов

Анализ и синтез гидропульсационной машины, страница 7

j1	F_и2xН	F_и2yН	F_и3xН	F_и3yН	F_и4xН	F_и4y Н	F_и5yН	M_и1 Н m	M_и2 Н m	M_и3 Н m	M_и4 Н m
266,5273	6,0102	-97,6672	2,9914	-93,9041	-31,6057	-74,8331	-16,4613	-0,3851	-4,6036	-9,9862	-9,9862
280	20,7949	-95,3388	3,7425	-89,2103	-29,7128	-71,5968	-15,6592	-0,3103	-1,4075	-9,4904	-9,4904
300	42,2851	-83,9401	7,4947	-79,3693	-24,9874	-65,5015	-14,0486	-0,1704	2,8453	-8,4661	-8,4661
320	60,1113	-63,3512	12,8464	-64,6454	-18,0085	-56,1338	-11,7048	0,0371	6,3775	-6,9590	-6,9590
340	70,6721	-34,7825	17,3121	-43,1302	-8,9766	-40,9467	-8,2714	0,3204	9,0808	-4,7719	-4,7719
360	70,9778	-1,0519	17,8073	-14,2936	1,2205	-18,1352	-3,5084	0,6459	10,8971	-1,8126	-1,8126
20	59,7505	33,4443	11,6532	20,0000	11,0034	12,0179	2,5313	0,9294	11,8589	1,8094	1,8094
40	38,3569	63,8496	-1,8922	55,9143	18,7807	46,6523	9,4315	1,0441	12,0900	5,7883	5,7883
60	10,8012	86,6805	-20,4584	89,3328	23,9451	81,2479	16,4659	0,8551	11,7204	9,7096	9,7096
80	-17,5026	101,0204	-38,4180	117,2068	27,3929	111,0830	22,6599	0,2922	10,6866	13,1087	13,1087
96,1481	-37,3238	106,7816	-47,0689	133,4657	30,0383	128,0656	26,1244	-0,3849	9,0252	15,0425	15,0425
100	-41,9931	107,2090	-47,7784	136,0299	30,6831	130,5249	26,6073	-0,3844	8,3111	15,3247	15,3247
120	-59,1784	100,6138	-39,8390	134,1988	32,8062	125,0822	25,5549	-0,3824	3,0419	14,8708	14,8708
140	-63,1719	77,5171	-15,1719	101,2750	29,9343	86,6512	18,0014	-0,3870	-4,4665	10,7845	10,7845
160	-57,8848	39,7304	11,8091	41,9147	18,6762	27,2395	6,1440	-0,3996	-12,2128	4,0495	4,0495
180	-50,1907	-4,0699	25,5100	-22,1590	1,1635	-28,5527	-5,3401	-0,4111	-17,3109	-2,7841	-2,7841
200	-42,7156	-43,2790	23,7698	-68,8413	-15,6703	-63,6153	-13,0049	-0,4133	-18,2304	-7,5621	-7,5621
220	-33,2544	-72,0720	15,0074	-91,9744	-26,7582	-77,7542	-16,5171	-0,4073	-15,6353	-9,8670	-9,8670
240	-19,3299	-89,7253	7,0995	-98,1267	-31,6458	-79,4519	-17,3032	-0,3978	-11,1709	-10,4535	-10,4535
260	-0,7737	-97,2569	3,2766	-95,6608	-32,1173	-76,2384	-16,7744	-0,3881	-6,1968	-10,1738	-10,1738
266,5273	6,0102	-97,6672	2,9914	-93,9041	-31,6057	-74,8331	-16,4613	-0,3851	-4,6036	-9,9862	-9,9862

4.2 Определение уравновешивающего момента и реакций в кинематических парах аналитическим методом

4.2.1 Силовой анализ структурной группы 4-5

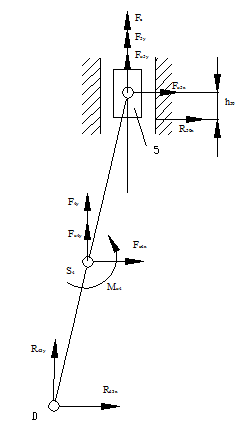Рисунок 4.1 - Действие сил на структурную группу 4-5

Уравнения равновесия группы 4-5:

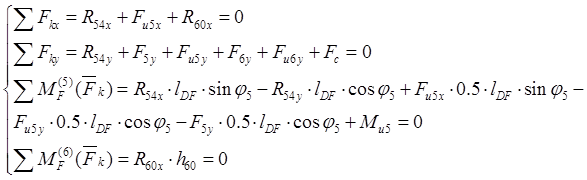Из 2- го ур-ния:

Из 3- го ур- ния:

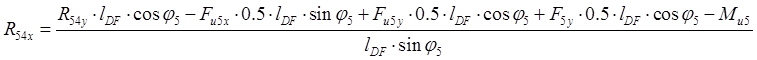Из 1- го ур- ния:

Реакция в поступательной паре F:

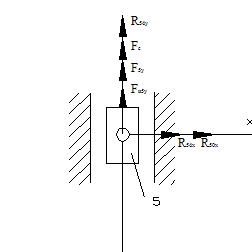Из 4- го ур- ния: h₅₀=0

Реакция в кинематической паре D:

Ревкцию во внутренней вращательной кинематической паре F определили из уравнений равновесия звена 6:

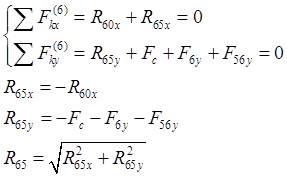Силовой анализ структурной группы 2-3

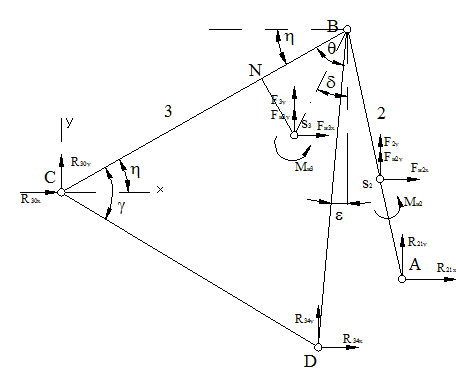Уравнения равновесия группы 2-3:

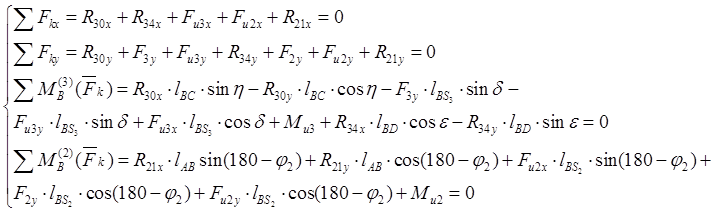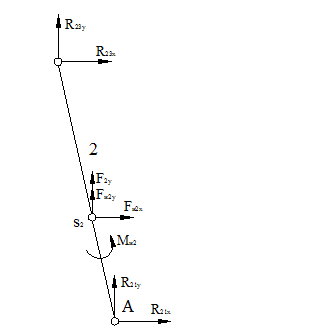Реакция в кинематической паре А:

Реакция в кинематической паре С:

Реакцию во внутренней кинематической паре В определяют из уравнений равновесия звена 2

Из 1-го ур- ния:

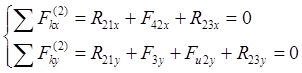Из второго ур- ния:

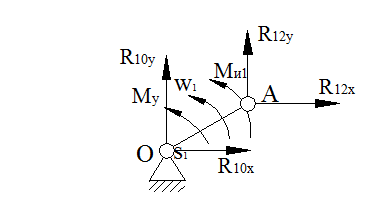
Силовой анализ начального звена:

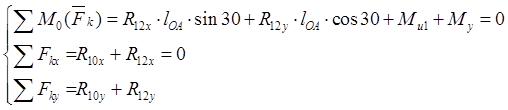Условия равновесия начального звена:

Из 1-го уравнения:

Из 2-го уравнения

Из 3-го уравнения :

Реакция в кинематической паре О:

Результаты расчетов сводят в таблицу 4.3

Таблица 4.3 - Реакции в кинематических парах и уравновешивающий момент

R₅₀,H	R₄₅,H	R₄₃,H	R₃₀,H	R₂₁,H	R₂₃,H	R₁₀,H	M_y,Hm
-3863,73	24362,39	24488,60	8677,47	21185,70	21,269,4276	21185,70	1039,91

1 2 3 4 5 6 7

Скачать файл