Машиностроение \ Теория машин и механизмов

Анализ и синтез гидропульсационной машины, страница 3

2.2.2 Определение аналогов скоростей

Для аналитического определения аналогов скоростей дифференцируют уравнения (2.5) (2.11), (2,15) и (2,15,1) по обобщенной координате

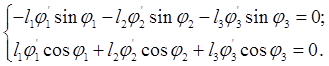(2.22)

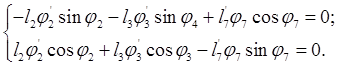(2.23)

Из системы уравнений (2.22) определяют j₂¢ и j₃¢

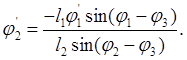(2.24)

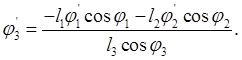(2.25)

Из уравнения (2.14) определяют j₄¢ :

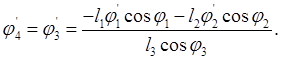Для определения и состовляют дополнительный замкнутый контур OCDFO

(2.26)

Проецируют на оси координат и дефференцируют:

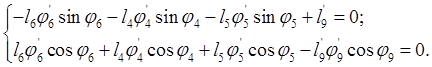(2.27)

Из (2.27) определяют и

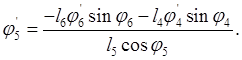Для аналитического определения аналогов скоростей центров масс дифференцируют системы уравнений (2.19) (2.20) и (2.21) по обобщенной координате

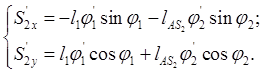(2.28)

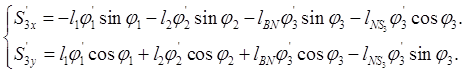(2.29)

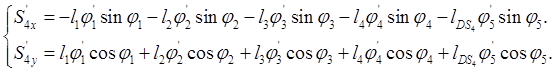(2.30)

(2.31)

Результаты расчетов аналогов скоростей сводят в таблицу 2.2.

Таблица 2.2 - Результаты расчета аналогов скоростей

j'₃	j'₂	j'₄	j'₅	L^'9	S'_2x	S'_2y	S'_3x	S'_3y	S'_4x	S'_4y	S'_5y
0,1407	0,0794	0,1407	0,0695	0,0419	-0,0087	0,0483	-0,0061	0,0364	0,0134	0,0599	0,0419
0,1387	-0,0007	0,1387	0,0608	0,0419	-0,0249	0,0433	-0,0087	0,0353	0,0118	0,0621	0,0419
0,0986	-0,0864	0,0986	0,0385	0,0301	-0,0338	0,0268	-0,0078	0,0246	0,0075	0,0457	0,0301
0,0197	-0,1652	0,0197	0,0072	0,0061	-0,0316	0,0023	-0,0017	0,0049	0,0014	0,0093	0,0061
-0,0792	-0,2123	-0,0792	-0,0299	-0,0243	-0,0195	-0,0244	0,0066	-0,0197	-0,0058	-0,0371	-0,0243
-0,1547	-0,1918	-0,1547	-0,0658	-0,0468	-0,0036	-0,0451	0,0104	-0,0392	-0,0127	-0,0699	-0,0468
-0,1675	-0,0949	-0,1675	-0,0821	-0,0499	0,0105	-0,0517	0,0075	-0,0433	-0,0158	-0,0716	-0,0499
-0,1244	0,0317	-0,1244	-0,0681	-0,0366	0,0215	-0,0427	0,0030	-0,0325	-0,0130	-0,0501	-0,0366
-0,0588	0,1318	-0,0588	-0,0342	-0,0172	0,0287	-0,0230	0,0007	-0,0154	-0,0065	-0,0227	-0,0172
0,0074	0,1817	0,0074	0,0044	0,0022	0,0297	0,0010	-0,0001	0,0019	0,0008	0,0028	0,0022
0,0663	0,1825	0,0663	0,0382	0,0194	0,0229	0,0240	-0,0009	0,0173	0,0073	0,0257	0,0194
0,1132	0,1443	0,1132	0,0615	0,0333	0,0090	0,0411	-0,0029	0,0295	0,0118	0,0458	0,0333
0,1407	0,0794	0,1407	0,0695	0,0419	-0,0087	0,0483	-0,0061	0,0364	0,0134	0,0599	0,0419

2.2.3 Определение аналогов ускорений

Для аналитического определения аналогов ускорений звена 2 и 3 дифференцируют систему уравнений (2.22)

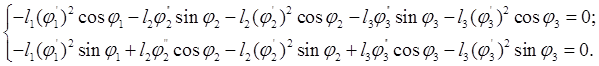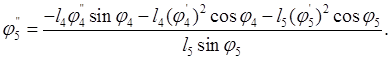(2.34)

(2.35)

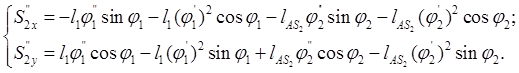(2.36)

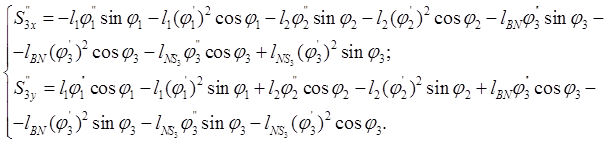
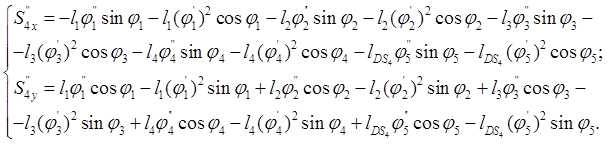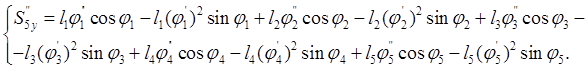Таблица 2.3 - Результаты расчета аналогов ускорений

j''₃	j''₂	j''₅	L^''9	S''_2x	S''_2y	S''_3x	S''_3y	S''_4x	S''_4y	S''_5y
0,0277	-0,1417	-0,0008	0,0090	-0,0343	0,0024	-0,0063	0,0063	-0,00001	0,0102	0,0092
-0,0382	-0,1613	-0,0311	-0,0209	-0,0257	-0,0211	-0,0025	-0,0109	-0,0059	-0,0089	-0,0104
-0,1156	-0,1624	-0,0525	-0,0531	-0,0070	-0,0406	0,0067	-0,0297	-0,0102	-0,0334	-0,0347
-0,1801	-0,1310	-0,0661	-0,0789	0,0149	-0,0512	0,0156	-0,0446	-0,0128	-0,0543	-0,0554
-0,1832	-0,0361	-0,0739	-0,0819	0,0292	-0,0482	0,0137	-0,0460	-0,0143	-0,0543	-0,0558
-0,0907	0,1187	-0,0566	-0,0454	0,0297	-0,0280	0,0000	-0,0246	-0,0109	-0,0239	-0,0260
0,0386	0,2343	-0,0017	0,0124	0,0239	0,0032	-0,0090	0,0087	-0,0001	0,0143	0,0129
0,1139	0,2299	0,0512	0,0498	0,0179	0,0295	-0,0068	0,0293	0,0100	0,0331	0,0341
0,1299	0,1456	0,0731	0,0596	0,0086	0,0436	-0,0024	0,0340	0,0139	0,0352	0,0381
0,1208	0,0459	0,0714	0,0560	-0,0053	0,0466	-0,0010	0,0316	0,0135	0,0321	0,0353
0,1029	-0,0395	0,0562	0,0469	-0,0204	0,0398	-0,0025	0,0269	0,0108	0,0281	0,0303
0,0740	-0,1024	0,0310	0,0318	-0,0316	0,0242	-0,0053	0,0190	0,0061	0,0219	0,0223
0,0277	-0,1417	-0,0008	0,0090	-0,0343	0,0024	-0,0063	0,0063	0,0000	0,0102	0,0092

1 2 3 4 5 6 7

Скачать файл

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание - внизу страницы.