Построим угловую характеристику мощности генераторов станции (рисунок 3.7).
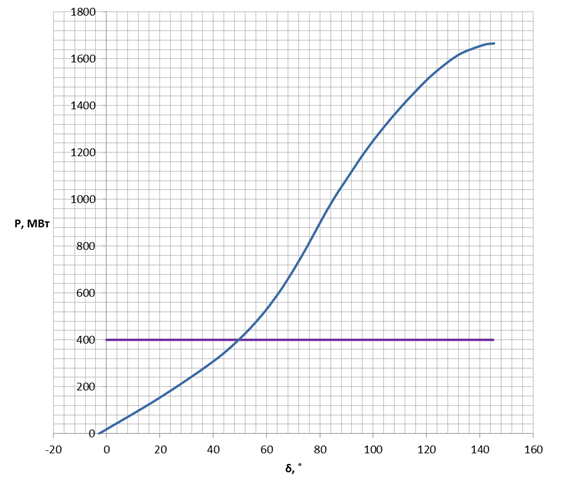
Рисунок 3.7 – Угловая характеристика мощности генераторов с АРВ ПД(ремонтная схема)
Имеем РМ = 1665,9 МВт ,dКР = 93,6°. Проверим погрешность снятия предельных значений мощности:
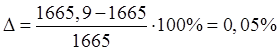
Погрешность расчета соответствует заданной.
Рассчитаем коэффициент запаса устойчивости. Для устойчивой системы в послеаварийном режиме его значение должно превышать 0,08:
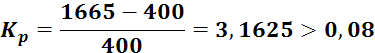
Система устойчива. Определим наибольшую мощность, которая может быть передана в систему:
МВт
Для большей наглядности различий в характеристиках, построим все 3 в одной системе координат (рисунок 3.8)
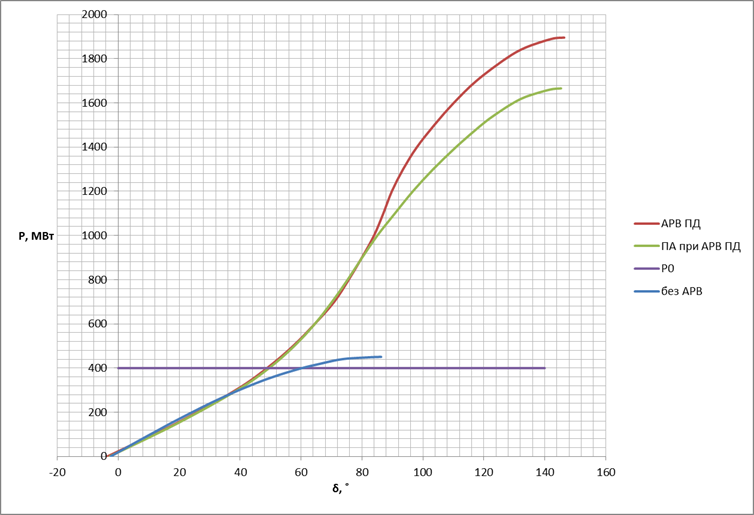
Рисунок 3.8 – Совмещённая угловая характеристика мощности генераторов
Проанализировав результаты исследования статической устойчивости электроэнергетической системы, можно заключить, что система устойчива во всех проверенных режимах. Также следует отметить, что наибольшим коэффициентом запаса устойчивости, наибольшей предельной передаваемой мощностью обладает нормальная схема с АРВ ПД.
4. РАСЧЕТ ПРЕДЕЛЬНОГО ВРЕМЕНИ ОТКЛЮЧЕНИЯ КОРОТКОГО ЗАМЫКАНИЯ
В качестве возмущения для исследования динамической устойчивости примем короткое замыкание на линии Л2 вблизи узла 5. Через некоторое время повреждённая линия отключается. Для оценки динамической устойчивости определим предельное время отключения короткого замыкания, при котором ещё сохранится динамическая устойчивость. Эту процедуру проводим в программе Mustang. Критерием устойчивости режима служит закон изменения угла δ во времени, где δ ‒ угол между ЭДС станции и напряжением балансирующего узла:
δij = δi – δj
Если разность с течением времени затухает, то режим устойчив, а если нет, то режим расходится.
Для начала расчёта необходимо изменить схему нормального режима работы системы с АРВ на генераторах. Заменяем сопротивление генераторных ветвей 8-9 и 10-6 с исходных на равные 0,001 Ом. Производим расчёт режима (рисунок 4.1).
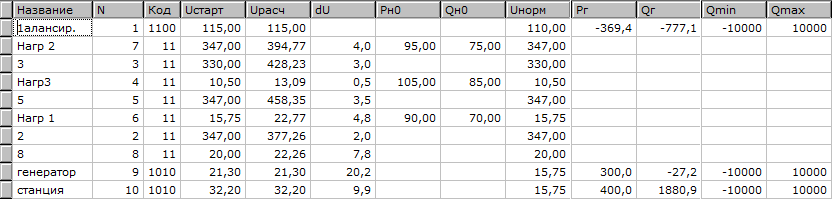
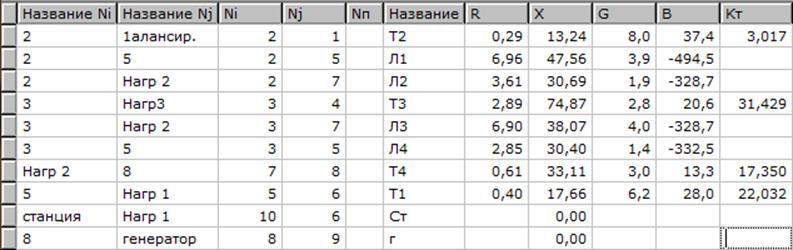Рисунок 4.1 – Исходные данные для расчёта схемы
Далее в разделе «Автоматика» моделируем желаемый процесс. Считаем, что в момент времени 0,2 с на линии Л2 вблизи 2-го узла произошло 3-х фазное КЗ. Через 0,2 с сработала автоматика, которая отключила линию (рисунок 4.2).
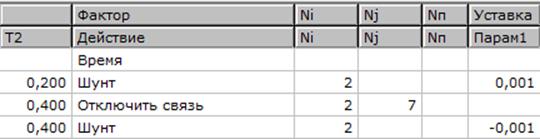
Рисунок 4.2 – Ввод действий автоматики
Затем заполним раздел «Генераторы» в именованных единицах (рисунок 4.3).
Рисунок 4.3 – Ввод данных о генераторах системы
Выберем необходимые для вывода данные в разделе «Контролируемые параметры» (рисунок 4.4).
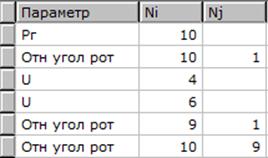
Рисунок 4.4 – Ввод контролируемых параметров
Задаёмся временем расчёта 5 с, шагом печати 0,01 с. В результате неоднократных расчётов с последовательным увеличением времени отключения линии, получим значение предельного времени отключения tо.пр.=0,397 с, при котором устойчивость ещё сохраняется. При tо.=0,398 с устойчивость системы нарушается.
Далее на рисунках 4.5 – 4.7 покажем графики зависимостей Рг10, U6, U4, δ10-1, δ10-1, δ10-9 от времени для tо.пр.=0,397 с и tо.=0,398 с соответственно.
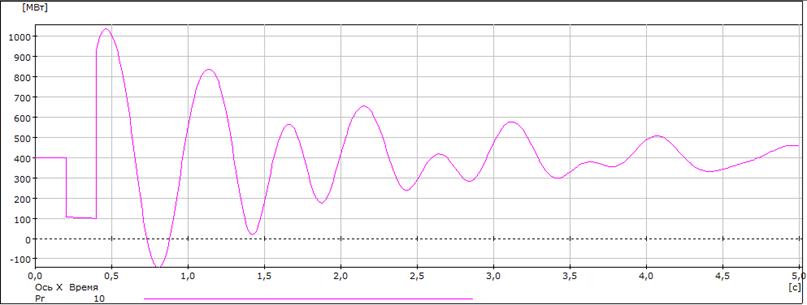
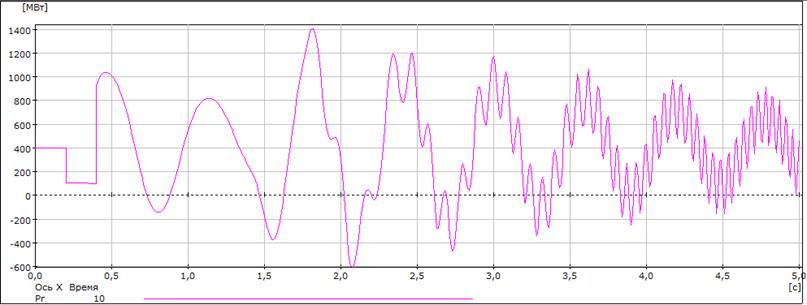
Рисунок 4.5 – Графики зависимостей Рг6 от времени дляtо.пр.=0,397 с и tо.=0,398 с
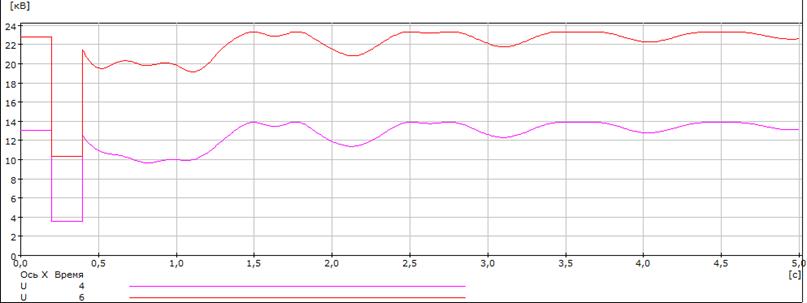
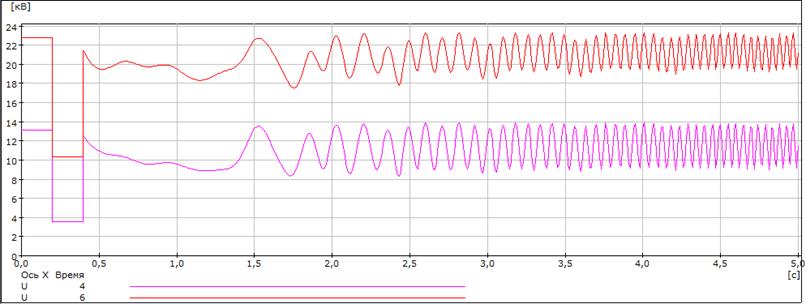
Рисунок 4.6 – Графики зависимостей U6 и U4от времени дляtо.пр.=0,397 с и tо.=0,398 с
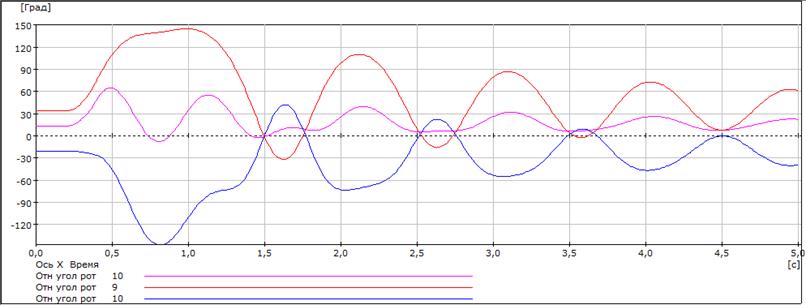
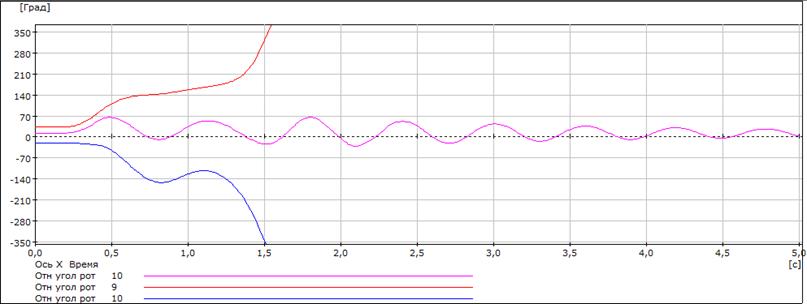
Рисунок 4.7 – Графики зависимостей δ10-1, δ10-1 и δ10-9 от времени дляtо.пр.=0,397 с и tо.=0,398 с
Определим точность расчёта ТОТКЛ. ПРЕД.:
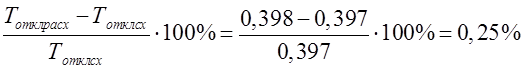
Заданная точность соблюдается.
Таким образом, в случае возникновения трёхфазного короткого замыкания на лини Л2 вблизи шин станции, для сохранения устойчивости системы необходимо произвести отключение линии за время, меньшее tо.пр.=0,397 с, иначе устойчивость системы будет нарушена.
Далее проанализируем влияние АПВ на динамическую устойчивость системы. На рисунке 4.8 показана последовательность действий автоматики при успешном АПВ. На рисунках 4.9 – 4.11 представлены изменения основных параметров во времени при успешном АПВ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.