Tjст=Tj×Pн×nт=6,8×200×2=2720 МВт×с;
Постоянная механической инерции генератора Г:
Tjг=Tj×Pн×nт=7×300×1=2100 МВт×с.
Расчёт будем производить в программе Mustang, поэтому перевод в относительные единицы не требуется.
2. Составление комплексной схемы замещения и расчет 3-х установившихся режимов электрической системы (нормальная схема с АРВ и без АРв генераторов, ремонтная схема с арв на генераторах)
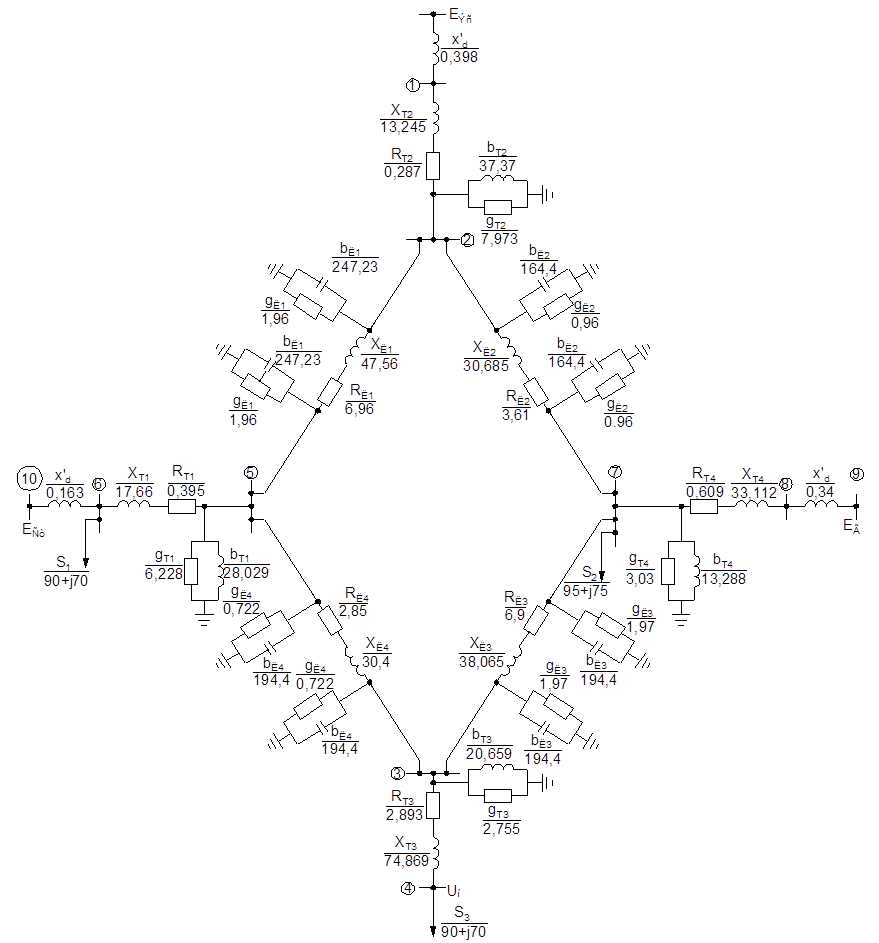
Рисунок 2.1- Комплексная схема замещения энергосистемы
Статическая устойчивость электроэнергетической системы - ее способность самостоятельно восстанавливать исходный установившийся режим при малых возмущениях или режим, весьма близкий к исходному, если возмущение не снято. Поскольку в электрической системе постоянно происходят малые возмущения, то статическая устойчивость является необходимым условием ее функционирования.
Статическую устойчивость системы будем оценивать по критерию (стр.31 [1]):
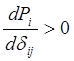, где 
- активная мощность исследуемой i - станции (генератора);
- угол
сдвига векторов ЭДС i
- й и j - й станции (генератора).
Расчет нормальной схемы электрической системы без АРВ пропорционального действия на генераторах станции
Схема замещения представлена на рисунке 2.1. В расчетах статической устойчивости генератор Г в 8-м узле представляем генератором с внутренним сопротивлением Х’dг=0,34 и добавляем точку 9,т.о. сопротивление генератора Г (ветвь 8-9) в режиме с АРВ задаём Xdг’= 0,34. В качестве сопротивления генераторов станции Ст (ветвь 6-10) в режиме без АРВ задаём Xdст= 0,98. В 10-ом узле устанавливаем напряжение E’ таким образом, чтобы напряжение в 6-ом узле U6=(1,05÷1,1)Uн. Исходные данные для расчёта нормальной схемы без АРВ в программе Mustang представлены на рисунке 2.2.
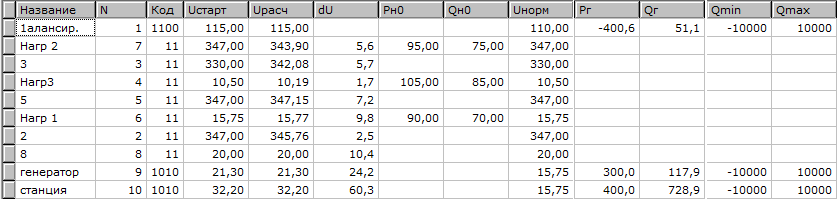
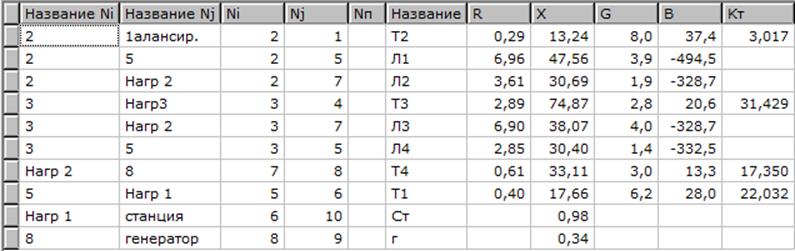
Рисунок 2.2 - Исходные данные для расчёта нормальной схемы без АРВ
Результаты расчёта представлены на рисунке 2.3
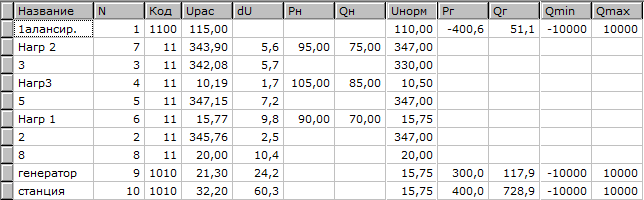
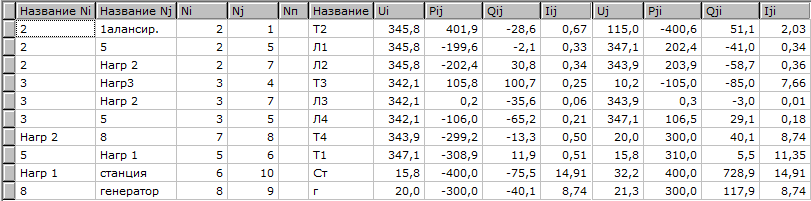
Рисунок 2.3 - Результаты расчёта нормальной схемы без АРВ
Итерационный процесс расчёта сходится при заданной номинальной мощности станции Ст. Напряжения в узлах находятся в допустимых пределах.
Расчет нормальной схемы электрической системы с АРВ
Схема замещения имеет вид как и при расчёте с АРВ ПД. Сопротивление генераторов станции Ст (ветвь 6-10) в режиме с АРВ будет равно синхронному сопротивлению X’dст= 0,163. В 9-ом узле задаём ЭДС E=(1,1÷4)Uн таким образом, чтобы напряжения в узлах лежали в допустимых пределах. Исходные данные для расчёта нормальной схемы с АРВ в программе Mustang представлены на рисунке 2.4.
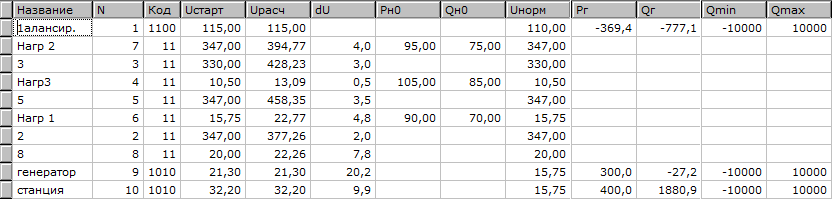
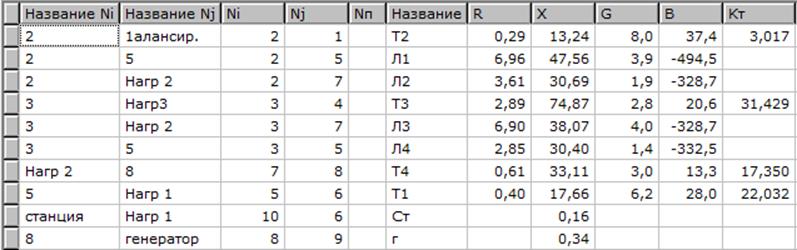
Рисунок 2.4 - Исходные данные для расчёта нормальной схемы с АРВ
Результаты расчёта представлены на рисунке 2.5
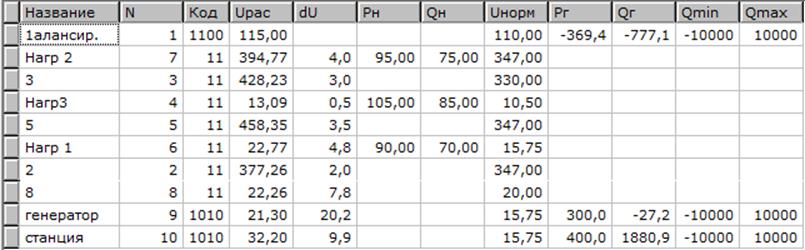
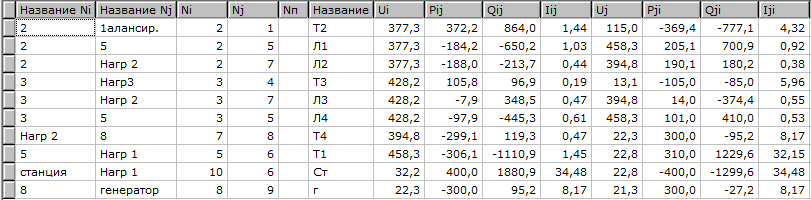
Рисунок 2.5 - Результаты расчёта нормальной схемы с АРВ
Расчёт ремонтной схемы системы с генераторами с АРВ ПД
Для расчёта ремонтной схемы работы системы с генераторами, снабжёнными АРВ ПД, отключим наиболее нагруженную ветвь 2-5 (линия Л2) и повторим расчёт. Исходные данные показаны на рисунке 2.6
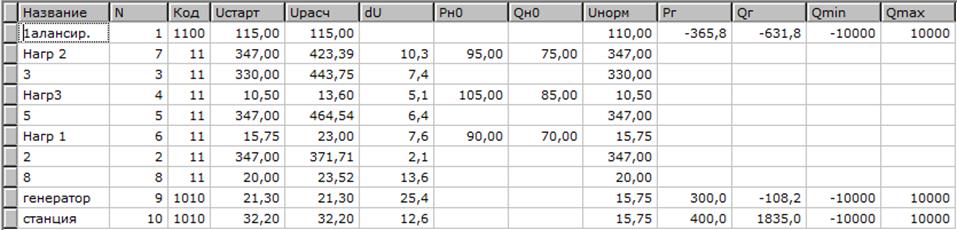
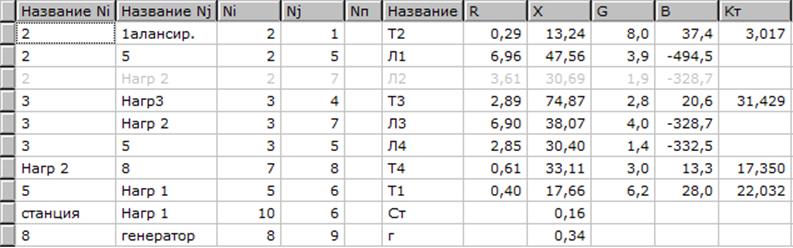
Рисунок 2.6 - Исходные данные для расчёта ремонтной схемы с АРВ
Результаты расчёта приведены на рисунке 2.7
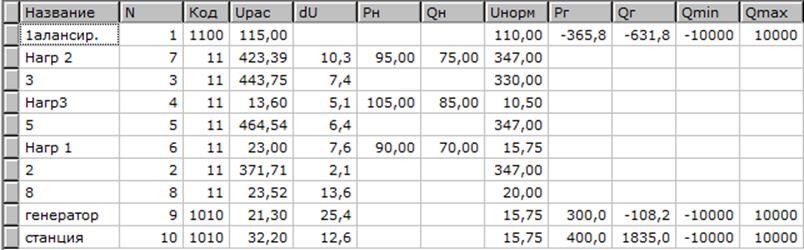
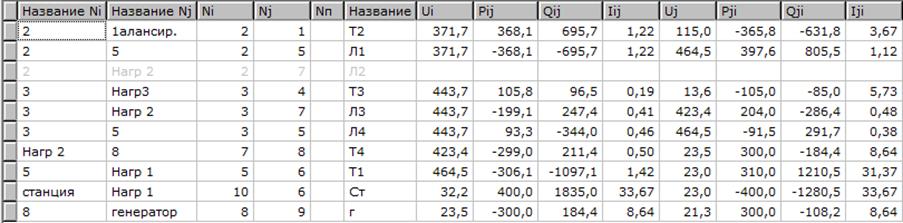
Рисунок 2.7 - Результаты расчёта ремонтной схемы с АРВ
3. Построение 3-х угловых характеристик, определение предела передаваемой мощности для нормальной и ремонтно-аварийной схем энергосистемы по условиям статической устойчивости
Угловые характеристики построим проведя расчёты в программе Mustang. Изменяя величину активной мощности (в 10-ом узле), получаем различные значения угла δ. Генерируемую мощность станции увеличиваем, пока итерационный процесс не разойдется, что свидетельствует о том, что заданная мощность больше предела системы и режима не существует.
Массивы значений P, Q, угла δ, необходимых для расчёта и построения угловой характеристики мощности генераторов с АРВ ПД в нормальном режиме в программе Microsoft Excel, приведены в таблице 3.1:
Таблица 3.1 – Массивы полученных значений Pг, d
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.