Министерство высшего образования РФ
НГТУ
Расчетно-графическое задание по дисциплине
«Элементы микросистемной техники»
Проектирование интеллектуального кремниевого сенсора давления
с упругим элементом прямоугольной формы.
|
Факультет |
РЭФ |
|
Группа |
РММ2-41 |
|
Студент |
Чебанов М.А., Танайно А.М. |
|
Преподаватель |
Гридчин В.А. |
|
Содержание. |
|
|
1. Техническое задание…………………………………………………... |
3 |
|
2. Проектирование упругого элемента………………………………….. |
4 |
|
Расчет прогибов упругого элемента методом Галеркина – Ритца…. |
4 |
|
Расчет напряжений и деформаций упругого элемента……………... |
10 |
|
3. Выбор оптимального расположения тензорезистивного моста на поверхности сенсора……………………………………………………... |
14 |
|
4. Расчет размеров тензорезисторов…………………………………….. |
18 |
|
5. Расчёт преобразовательной характеристики сенсора……………….. |
22 |
|
6. Схема технологического маршрута…………………………………... |
23 |
|
7. Литература……………………………………………………………... |
26 |
Техническое задание.
1. Провести проектирование упругого элемента сенсора давления.
2. Провести проектирование топологии электрической схемы сенсора.
3. Разработать схему технологического маршрута изготовления сенсора, включающую формирование электрической схемы и профилирование упругого элемента.
|
Исходные данные для РГЗ: |
|
|
1. Номинальное давление |
2 атм. |
|
2. Коэффициент запаса прочности |
1.5 |
|
3. Форма упругого элемента |
Прямоугольная |
|
4. Геометрические размеры упругого элемнта |
3:1 |
|
5. Кристаллографическая плоскость |
110 |
|
6. Тип проводимости тензорезисторов |
Р |
|
7. Номинальное значение сопротивления тензорезисторов |
100 Ом |
|
8. Закон распределения примеси |
Гауссово |
|
9. Максимальная концентрация легирующей примеси |
2*1019 1/см3 |
|
10. Напряжение питания мостовой схемы |
5 В |
Проектирование упругого элемента.
Расчет прогибов упругого элемента методом Галеркина – Ритца.
Задача расчета напряжений и деформаций сводится к
решению уравнения на прогибы ![]() пластины с
соответствующими граничными условиями:
пластины с
соответствующими граничными условиями:
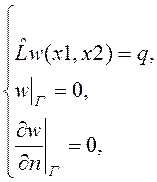 (1)
(1)
где
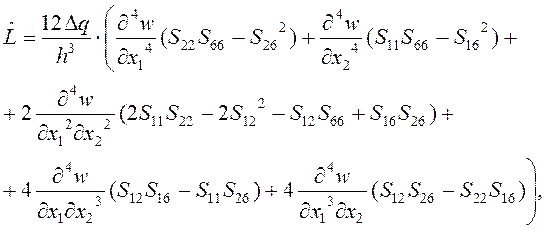 (2)
(2)
Г – контур
пластины и ![]() - нормаль к контуру.
- нормаль к контуру.
Решение этой задачи может быть проведено различными методами:
1) интегрированием с применением двойных рядов Фурье;
2) применением методов конечных разностей и конечных элементов;
3) использование вариационных принципов механики.
Вариационные методы решения чрезвычайно удобны для микросистемной техники, поскольку позволяют получить результаты в аналитической форме и с приемлемой для техники точностью. Существует несколько модификаций вариационных методов решения: энергетический, метод Галеркина-Ритца, комбинированный метод Л. В. Конторовича, метод обращения, эффективность применения которых зависит от конкретной формулировки задачи.
Для случаев малых прогибов квадратных и прямоугольных упругих элементов весьма эффективен метод Галеркина-Ритца.
Уравнение на прогибы для прямоугольной балки имеет следующий вид:
![]() , (3)
, (3)
где ![]() и
и ![]() –
половины сторон пластин вдоль х1 и х2 соответственно;
коэффициенты
–
половины сторон пластин вдоль х1 и х2 соответственно;
коэффициенты ![]() должны быть подобраны исходя из
минимальности интеграла:
должны быть подобраны исходя из
минимальности интеграла:
![]() (4)
(4)
Используя
вариационное условие (4), получаем систему линейных уравнений для определения
коэффициентов ![]() :
:
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
(5)
,
(5)
![]() ,
,
![]() .
.
Введем безразмерные координаты
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
В новых
обозначениях оператор ![]() имеет вид
имеет вид
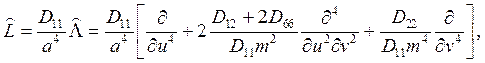 (6)
(6)
где ![]() - изгибные жесткости анизотропной пластины,
выражающиеся через упругие податливости кремния в системе координат, связанной
со сторонами пластины:
- изгибные жесткости анизотропной пластины,
выражающиеся через упругие податливости кремния в системе координат, связанной
со сторонами пластины:
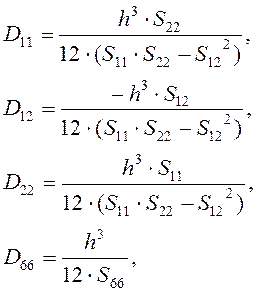 (7)
(7)
где ![]() - компоненты упругой податливости,
пересчитанные в системе координат сторонами упругого элемента Рис. 1.
- компоненты упругой податливости,
пересчитанные в системе координат сторонами упругого элемента Рис. 1.
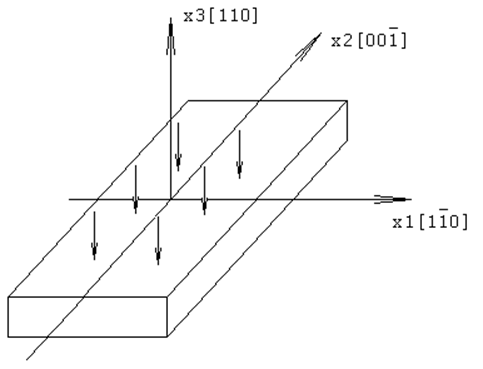
Рис. 1. Схематичное изображение нагруженного упругого элемента, с выбранной системой координат.
Ориентация сторон пластины выберем вдоль кристаллографических направлений показанных на Рис. 1. Систему координат свяжем со срединной плоскостью, а начало координат поместим в центр пластины.
В выбранной
системе координат пластины обладают ортотропной упругой симметрией и компоненты
матрицы упругих податливостей ![]() и
и ![]() равны нулю.
равны нулю.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.