Проектирование интеллектуального кремниевого сенсора давления с упругим элементом прямоугольной формы, страница 4

Результат выполнения функции Minimize выглядит следующим образом:

Minimize(,)=.

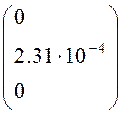Этот результат следует интерпретировать следующим образом:

Тензорезистор, который будет уменьшать сопротивление должен иметь угол =0 и координаты x1 = м и x2 = 0.

При таких параметрах 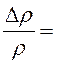 -0,016.

Относительное изменение сопротивления тензорезисторов, которые будут увеличивать сопротивление сильно отличается от относительного изменения сопротивления тензорезисторов, которые будут уменьшать сопротивления по модулю. Такой результат сильно противоречит условию линейности (20). Следовательно надо уменьшать разность в относительных изменениях сопротивлениях, путем перемещения тензорезистора, который увеличивает сопротивление вдоль оси x1 по направлению к центру мембраны. Это перемещение надо осуществлять до тех пор, пока относительные сопротивления тензорезисторов не сравняются. Рассчитать следующее положение тензорезистора, который увеличивает сопротивление можно также с помощью функции Maximize, просто добавив ограничение

В итоге получили следующие параметры  расположения тензорезистора, который увеличивает сопротивление: угол =0 и координаты x1 = м и x2 = 0.

Следовательно, примерная схема расположения тензорезисторов на нашем прямоугольном упругом элементе может выглядеть как показано на Рис. 15.

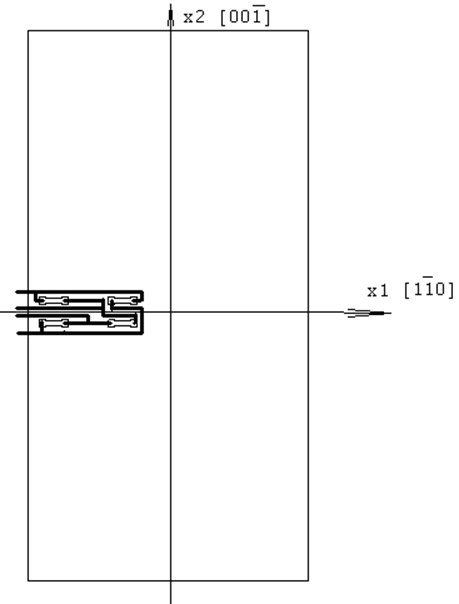
Рис. 15. Оптимальный вариант размещения тензорезистивного моста.

Расчет размеров тензорезисторов.

Для того чтобы рассчитать поверхностное сопротивление p-Si необходимо знать его среднее удельное сопротивление. Распределения примеси имеет  неоднородный характер и выражается функцией Гаусса:

N(x)=N₀·exp(-x²/L²), где L²=4*D*t – характеристическая длина.

В нашем случае зададимся глубиной залегания p-n-перехода = 1мкм и концентрацией в подложке = 10¹⁵ 1/см³, тогда используя формулу Гауссово распределения получим профиль распределения концентрации примеси представленный на Рис. 16.

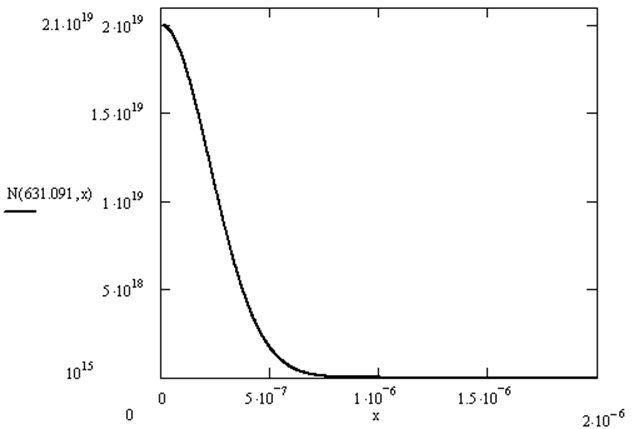
Рис. 16. Профиль распределения концентрации примеси.

Где первый параметр в функции N представленной на Рис. 16 – это расчетное время разгонки примеси, т.е 631,091с ≈ 10,5мин.

Для нахождения среднего удельного сопротивления составим программу, задачей которой будет вычисление среднего значения электропроводности, определенной формулой 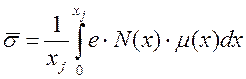(30).

                                                                          (30)

Для нашей задачи удобней будет использовать следующий вид формулы (30):

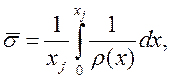
т.к. на кафедре ПП и МЭ А.В. Барановой были получены температурно-концентрационные двухмерные сплайн модели удельного сопротивления p- и n-Si Барановой, реализованные в модуле Si2.cpp.

Основываясь на этих данных модульная структура нашей программы представлена на Рис. 17.

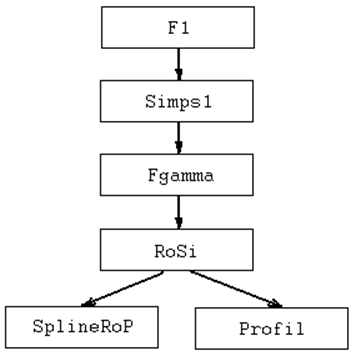
Рис. 17. Модульная структура программы расчета средней электропроводности.

Модуль F1 отвечает за расчет интеграла (30), Simps1 представляет собой модуль расчета определенных интегралов методом Симпсона, Fgamma –  подынтегральная функция, RoSi – функция расчета удельного сопротивления кремния, SiplineRoP – сплайн модель удельного сопротивления кремния p-типа, Profil – функция расчета  профиля концентрации легирующей примеси.

В управляющей программе достаточно вычислить обратное значение электропроводности чтобы получить среднее значение удельного сопротивления.

Результатом выполнения программы являются следующие данные:

Average Ro:

0.0232866

Для продолжения нажмите любую клавишу . . .

Следовательно среднее удельное сопротивление = 2.3*10^-2 Oм*см.

Полученный результат соответствует данным представленным на Рис. 18, где изображены кривые Ирвина.

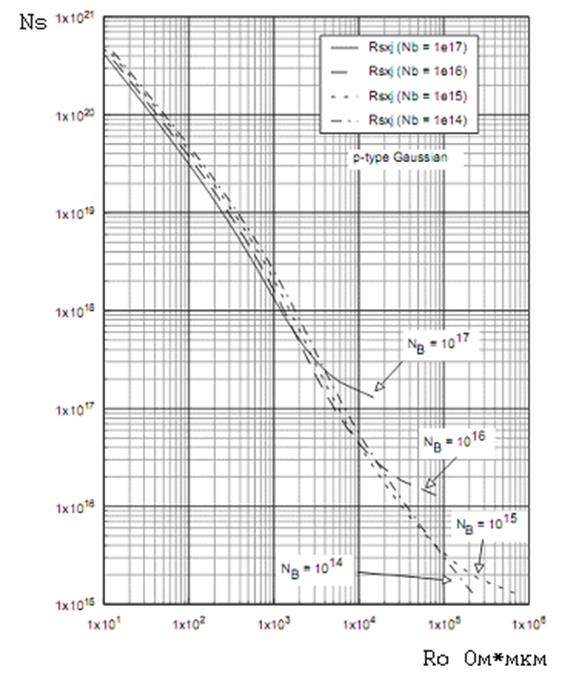
Рис. 18. Кривые Ирвина для p-Si.

Найдем поверхностное сопротивление:

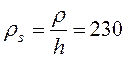Oм/кв.

Форма тензорезистора типа собачья кость Рис. 19.

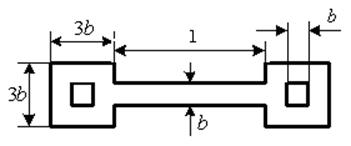
Рис. 19. Форма тензорезистора.