Проектирование интеллектуального кремниевого сенсора давления с упругим элементом прямоугольной формы, страница 2

Для кристаллов обладающих, симметрией кремния для пересчета компонент тензора упругой податливости, удобно использовать следующую формулу

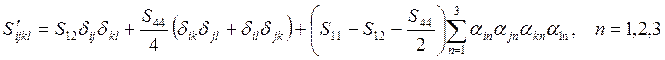.   (8)

где  - компоненты тензора упругих податливостей в новой системе координат; [] - матрица направляющих косинусов;  - символ Кронекера.

Переход от тензорных обозначений к матричным происходит по следующему правилу:

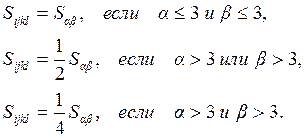                                                                  (9)

Матрица направляющих косинусов  используется для перехода от одной системы координат к другой и имеет следующий вид:

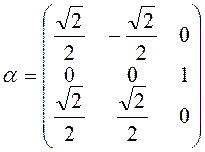.                                                                                (10)

В плоскости (100) компоненты упругой податливости имеют следующие значения:

S₁₁=0,774∙10^-11 м²/Н;

S₁₂=-0,216∙10^-11 м²/Н;

S₄₄=1,26∙10^-11 м²/Н;

S₂₂=0,768∙10^-11 м²/Н;

S₆₆=1,26∙10^-11 м²/Н;

Используя формулу (8) условие (9) и матрицу направляющих косинусов (10), пересчитываем компоненты упругой податливости для плоскости (110):

S^’₁₁=0,594∙10^-11 м²/Н;

S^’₁₂=-0,216∙10^-11 м²/Н;

S^’₄₄=1,26∙10^-11 м²/Н;

S^’₂₂=0,774∙10^-11 м²/Н;

S^’₆₆=1,26∙10^-11 м²/Н;

Производим расчет компонент тензора изгибных жесткостей  по формуле (7):

5,166∙10^-4 Па^-1;

3,926∙10^-4 Па^-1;

1,428∙10^-4 Па^-1;

2,116∙10^-4 Па^-1,

В формуле (7) использовали h = 32∙10^-6 м. Дальше будет показано что такая высота упругого элемента не противоречит условию запаса прочности.

Прогибы пластины могут быть представлены в форме

                                                                  (11)

где 

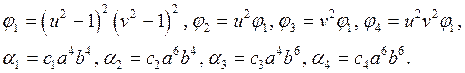
Система уравнений (5) в новых обозначения принимает вид:

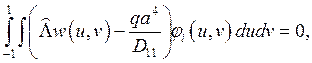                                                          (12)

где оператор  определен выражением в квадратных скобках (5).

Подставляя выражение для прогибов (11) в (12), получаем линейную систему алгебраических уравнений:

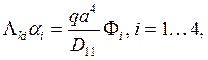                                                                         (13)

где - матричные элементы системы уравнений:

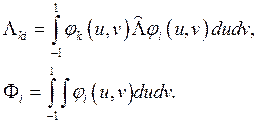                                                                 (14)

Для выбранной системы функций (5) матричные элементы системы уравнений (13) соответственно равны.

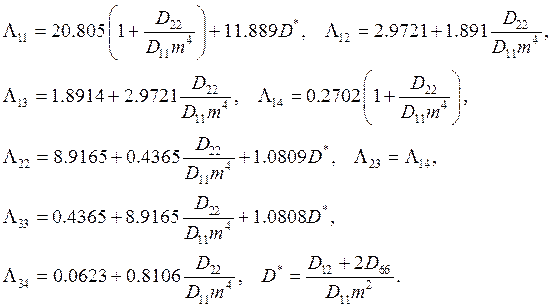
В силу эрмитовости оператора  матрица коэффициентов  оказывается симметричной. Интегралы в правой части системы (13) оказываются равны

Коэффициенты  определяем из системы (13) и выразив их из a:

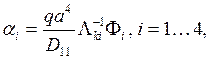 где

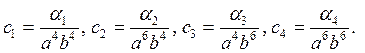
Выбрав следующие геометрические параметры упругого элементна: , ; получили  следующие результаты:

Подставляя полученные значения коэффициентов в формулу (3) строим график распределения прогибов по поверхности упругого элемента Рис. 2.

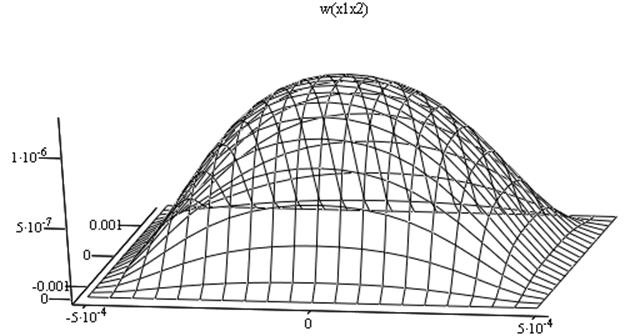
Рис. 2. График функции прогибов.

Используя Рис. 2 проверим выполнение условия малых прогибов:

                                                                                           (15)

Расчет напряжений и деформаций упругого элемента.

Формулы  для вычисления деформаций:

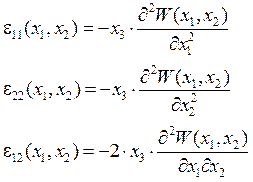,                                                                 (16)

где  .

Используя программу MathCad получаем следующие графики распределения компонент тензора деформации по поверхности мембраны:

Рис. 3. Распределение компоненты по поверхности мембраны.	Рис. 4. Распределение компоненты вдоль оси x1 при x2=0.
Рис. 5. Распределение компоненты по поверхности мембраны.	Рис. 6. Распределение компоненты вдоль оси x2 при x1=0.
Рис. 7. Распределение компоненты по поверхности мембраны.	Рис. 8. Распределение компоненты вдоль оси x2 при x1=0,00035.

Из графиков представленных выше видно что максимальное значение механической деформации проявляется у компоненты  на границах упругого элемента. Проверим условие запаса прочности: