Проектирование сенсора механической величины

Министерство образования Российской Федерации

Новосибирский Государственный технический университет

Кафедра полупроводниковых приборов и микроэлектроники

Курсовая работа

Проектирование сенсора механической величины

Факультет: РЭФ

Студент: Сорокин И.С.

Преподаватель: Гридчин В.А.

Дата:

Отметка о защите:

Новосибирск

2003

Содержание

1. Техническое задание. 3

2. Распределение напряжений и деформаций по квадратному упругому элементу. 4

2.1. Расчет прогибов упругого элемента. 4

2.2. Расчет механических напряжений и деформаций. 7

3. Проектирование топологии тензорезистивного моста. 12

3.1. Расчет сопротивлений тензорезисторов. 12

2. Проектирование топологии сенсора. 14

4. Проектирование технологического маршрута изготовления сенсора давления. 17

5. Расчет преобразовательной характеристики сенсора. 21

6. Список литературы.. 22

1. Техническое задание

1.  Тип плоскости: (100).

2.  Тип упругого элемента: квадрат.

3.  Тип тензорезисторов: n-тип.

4.  Поверхностная концентрация примеси 2×10¹⁹ см^-3.

5.  Характеристический размер упругого элемента: 2´2 мм².

6.  Номинальное давление: 1 атм.

7.  Сопротивление тензорезисторов: 1000 Ом.

8.  Перегрузочная способность: 2.

9.  Напряжение питания: 5 В.

10. Выходной сигнал не менее 20 мВ.

2. Распределение напряжений и деформаций по квадратному упругому элементу

2.1. Расчет прогибов упругого элемента

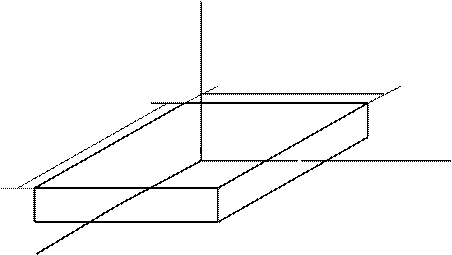
Для нахождения распределений прогибов в упругом элементе прямоугольной формы при равномерно распределенной нагрузке воспользуемся методом Галеркина – Ритца.

 

2а

2a

 

Рис.1. Схема упругого  жестко защемленного элемента.

При измерениях давления на такую пластинку действует равномерно распределенная нагрузка интенсивностью q. Расчет напряжений и деформаций сводится к решению уравнения на прогибы w(x1,x2) пластины с соответствующими граничными условиями:

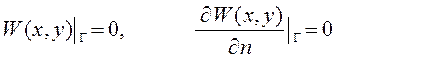,                                               (1)

Г – контур пластины и  - нормаль к контуру.

Начало координат выбираем в центре недеформированной мембраны, а оси направляем параллельно сторонам упругого элемента.

В выбранной системе координат пластины обладают ортотропной симметрией и компоненты матрицы упругих податливостей S₁₆ и S₂₆ равны нулю. В этом случае оператор  принимает вид

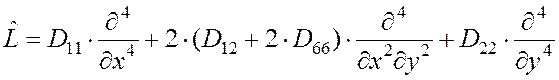                         (2)

Здесь D_ij – изгибные жесткости анизотропной пластины, выражающиеся через упругие податливости в системе координат, связанной со сторонами пластины:

; ;

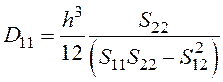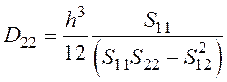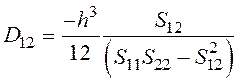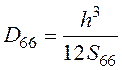; ,                                    (3)

S_ij - коэффициенты тензора упругих податливостей, связанные со сторонами пластины.

Граничные условия применительно к рассматриваемому случаю имеют вид:

;

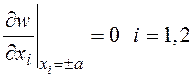
Для квадратной пластины прогибы будем искать в виде:

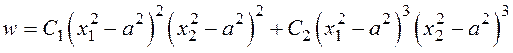,            (4)

где  и  неизвестные коэффициенты, подлежащие определению. Коэффициенты  и определяем из системы:

;

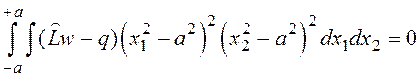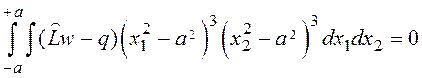.                                     (5)

Для удобства расчетов приведем выражения компонент тензора напряжений через прогибы:

;

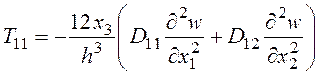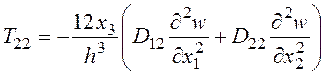                                        ;                                      (6)

.

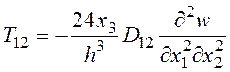Толщины тензорезистивного слоя много меньше толщины пластины, так что для проектирования  сенсоров давления можно принять координату  равной 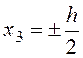. В этом случае компоненты .

Решение системы уравнений (5) с учетом (6) дает следующие выражения для коэффициентов  пластины со стороной :

; ;

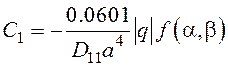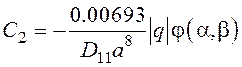где:

;

;

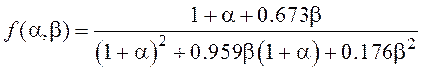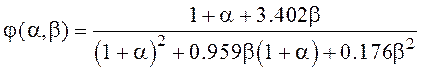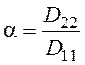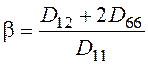;   .                                             (7)

Параметры a, h подбираем согласно условию малых прогибов:

W(0,0) < .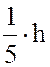

С учетом технического задания выбраны следующие параметры упругого элемента: a = 1 мм; h = 40 мкм.

2.2. Расчет механических напряжений и деформаций

Коэффициенты тензора упругих податливостей описывают механические свойства материала. Обычно в литературе приводятся данные для системы координат, связанной с ориентацией пластины (100) и направлением [100]. Часто возникает необходимость пересчета коэффициентов тензора упругих податливостей при переходе в новую систему координат. Для этого необходимо найти матрицу перехода от старой системы координат к новой:

Матрица поворота имеет вид:

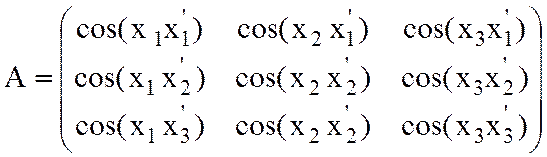                    (1)

Выберем следующие направления осей в новой системе координат: х¢₁ – [], х¢₂ – [], x¢₃ - [].

Для пересчета S_ij воспользуемся формулой:

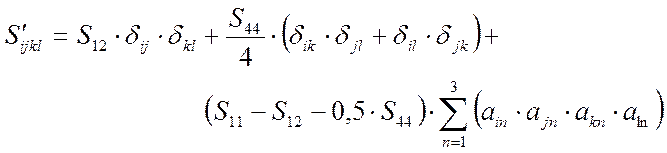,                (2)                                                                         

где a_mn – элементы матрицы перехода от системы связанной с ориентацией элементарной ячейки к системе связанной с ориентацией сторон упругого элемента; S_ij – коэффициенты тензора упругих податливостей в плоскости (100) и направлении [100].

Рассчитаем коэффициенты тензора упругих податливостей для     плоскости (100) и указанных направлений.

Vатрицf перехода:

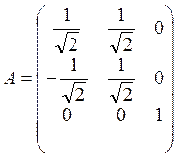
В плоскости (100) и направление [100] компоненты тензора упругих податливостей имеют следующие значения: