Проектирование сенсора механической величины, страница 2

S₁₁ = 0,7691·10^-11 м²/H,

S₁₂ = - 0,214·10^-11 м²/H,

S₄₄ = 1,257·10^-11 м²/H.

Найдем компоненты тензора упругих податливостей, которые нам в дальнейшем понадобятся для расчетов прогибов, деформаций, напряжений:

S₁₁¢=S₁₂+0,5·S₄₄+( S₁₁-S₁₂-0,5·S₄₄)·(a₁₁⁴+ a₁₂⁴ +a₁₃⁴) =0,5·( S₁₁+S₁₂)+0,25·S₄₄

S₁₂¢=S₁₂+( S₁₁-S₁₂-0,5·S₄₄)·(a₁₁²·a₂₁²+ a₁₂² ·a₂₂² +a₁₃² ·a₂₃²) =0,5·( S₁₁+S₁₂)-0,25·S₄₄

S₂₂¢= S₁₂+0,5·S₄₄+(S₁₁-S₁₂-0,5·S₄₄)·(a₂₁⁴+a₂₂⁴ +a₂₃⁴) = 0,5·( S₁₁+S₁₂)+0,25·S₄₄

S₆₆¢= S₄₄+4· ( S₁₁-S₁₂-0,5·S₄₄)·( a₁₁²·a₂₁²+ a₁₂² ·a₂₂² +a₁₃² ·a₂₃²) =2·( S₁₁-S₁₂)

Компоненты тензора упругих податливостей для плоскости (100) и направления [110]:

S₁₁¢= 1,535·10^-11 м²/H,

S₁₂¢= -3,67·10^-13 м²/H,

S₂₂¢= 5,918·10^-12 м²/H,

S₆₆¢=1,966·10^-11 м²/H.

В результате расчетов получено максимальное значение прогиба (в центре) квадратного упругого элемента при заданных параметрах W(0,0)=2,849×10^-8 м, что не противоречит условию малых прогибов (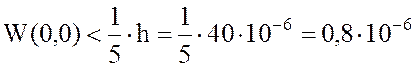м).

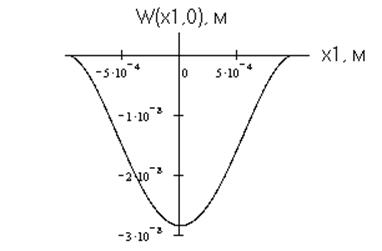
Рис. 2. Прогиб квадратного упругого элемента вдоль оси х₁ под действием равномерно распределенного давления.

Выражения для вычисления деформаций имеют вид: 

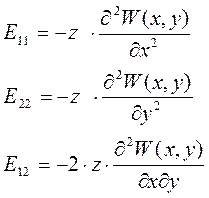                                                                                   (3)

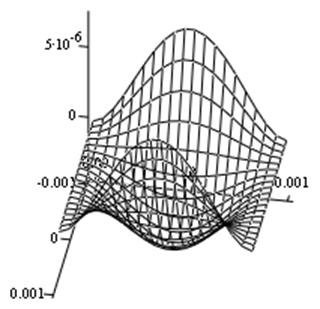
Рис. 5. Компонента Е₁₁ тензора деформаций.

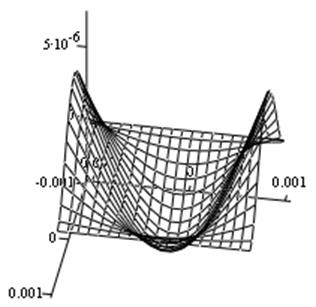
Рис. 6. Компонента Е₂₂ тензора деформаций.

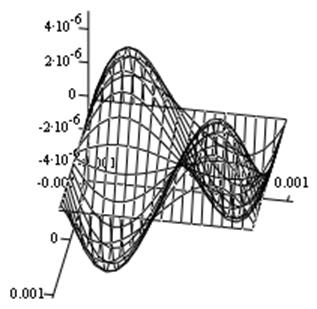
Рис. 7. Компонента Е₁₂ тензора деформаций.

Максимальная деформация, возникающая в упругом элементе при максимальном давлении с учётом коэффициента запаса равна E_max=1,687×10^-6, что не превышает максимально возможных деформаций E_max£2×10^-3.

Зная распределение прогибов упругого элемента можно также найти распределение механических напряжений. Для нахождения выходного сигнала нам понадобятся Т₁₁, Т₂₂ и Т₁₂ .

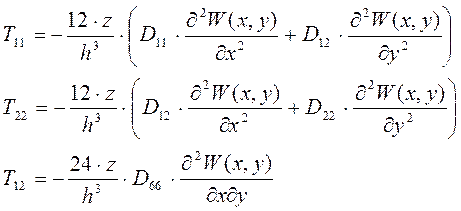                                         (4)

Получаем следующее распределение механических напряжений на верхней поверхности упругого элемента, т.е. при z=h/2:

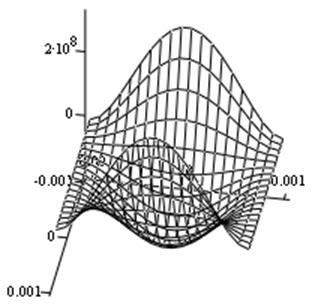
Рис. 8. Компонента Т₁₁ тензора напряжений.

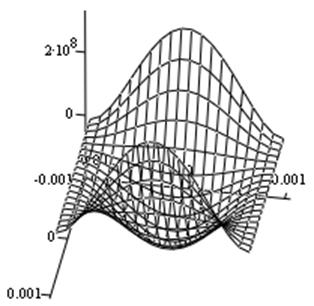
Рис. 9. Компонента Т₂₂ (б) тензора напряжений.

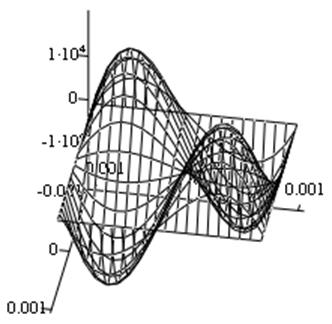
Рис. 10. Компонента Т₁₂.

3. Проектирование топологии тензорезистивного моста

3.1. Расчет сопротивлений тензорезисторов

Тензорезистор неоднородно легирован по толщине и имеет гауссово распределение примеси:

N_a(x)=N₀·exp(-x²/L²).                                                                        

Неоднородное легирование тензорезистора по толщине приводит к тому, что удельное сопротивление ненагруженного тензорезистора и коэффициент продольного пьезосопротивления изменяется с координатой х.Сопротивление тензорезистора определяется, в основном, узкой частью его тела, можно считать, что линии тока параллельны поверхности. Систему координат выбираем следующим образом, ось y направлена вдоль длинной оси, а ось x- вглубь от поверхности. В направлении x изменяется концентрация легирующей примеси, т. е. тензорезистор оказывается неоднородно легирован по толщине.

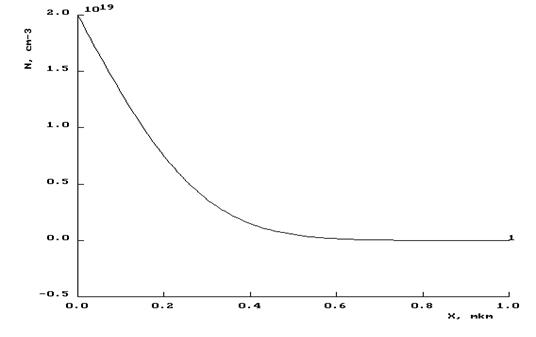
Рис. 11. Распределение примеси по глубине.

Возьмем бесконечно тонкий слой тела тензорезистора толщиной dx. Тогда удельное поверхностное сопротивление можно вычислить по формуле:

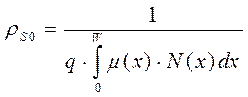                                                                             (1)

подвижность находим, используя модель Зильбергера, тогда элементарная проводимость имеет вид:

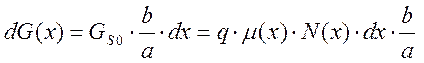                                                (2)

Проводимость всего тела тензорезистора определяется:

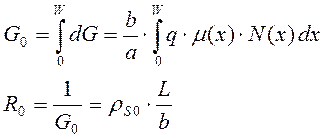                                                                (3)

a/b –число квадратов, укладывающихся на поверхности резистивного слоя, поэтому ρ_S0 имеет размерность Ом/□.

Теперь рассмотрим нагруженный тензорезистор:

При деформации тензорезистора меняется удельное сопротивление каждого элементарного слоя dx в направлении ℓ.