Оказывается значения Р(n) отражают флуктуацию относительно значения 0.5, но. главное, она слабеет с ростом n.
Говорят, что выполняется условие устойчивости: за кратким периодом иррегулярности следует длительный период регулярности. Флуктуации постепенно затухают для больших n. Именно в такого типа явлениях, когда из множества беспорядков возникает порядок, можно использовать в исследованиях методы теории вероятностей.
Рассмотренный тип регулярности появляется, например, при наблюдении срока службы электрических лампочек. Пусть x1, x2, … , xj,… обозначают наблюдаемые сроки службы лампочек, и пусть
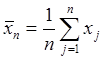 (1.2)
(1.2)
есть среднее арифметическое сроков службы первых n лампочек. Эмпирически установлена аналитическая сходимость на графике изменения хnс ростом n. Флуктуации затухают с ростом n и значение хп как бы стремиться к предельному значению.
интерпретируемому как «долговстречагюееся среднее» срока службы данного образца лампочек.
Замечание 1.1 Если в эксперименте подбрасывания монеты определить индикатор значений х, со значением 0 или 1 в зависимости от выпадения в j-ом опыте герба или решки, то придем к выводу, что значения, вычисленные по формулам (1.1) и (1.2) совпадают. Таким образом, аксиоматическую теорию можно строить на идеализации либо «долговстречающейся доли» (вероятности), либо «долговстречающегося среднего». Первый случай чаще используется в классической теории вероятностей.
Определение 1.2 Под опытом (экспериментом) надо понимать совокупность условий, когда наблюдается то или иное явление, его результат фиксируется.
Так вот, если результат неоднозначен, то мы будем подразумевать и рассматривать это как опыт со случайным исходом.
Как только мы допустим устойчивость частот в эксперименте, так мы принимаем некоторую случайную, но закономерность.
Коль скоро мы ожидаем частотной устойчивости, то надо определить, то, ради чего.
Определение .1.3 Случайное событие - это любая качественная характеристика опыта со случайным исходом, т. е. факт, который может произойти или не произойти.
Случайное событие (или просто событие) обычно обозначают большими буквами латинского алфавита. Примеры опытов и событий:
1. Например, происходит бросание монеты один раз; событие А - появление герба.
Будем писать А - {появление герба}.
2. Другой опыт: бросание правильной игральной кости один раз; событие В =
{появление шести очков или шестерки}.
Рассматривая введенные события А и В можно заметить, что каждое из них обладает различной степенью возможности появления. Событие А имеет большую степень появления, чем событие В. Любое случайное событие обладает какой-то степенью возможности появления, которую можно измерить численно, т.е. с возможностью появления (необходимостью появления) следует связать число, которое тем больше, чем более возможно появление события в опыте.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.