Практическое освоение методов многокритериальной оптимизации для линейного непрерывного случая.
Содержательная постановка линейной задачи многокритериальной оптимизации такова. Задана система ограничений вида:
|
|
(2.1) |
где ![]() —
множество — область допустимых решений;
—
множество — область допустимых решений; ![]() — вектор
свободных (управляемых) переменных;
— вектор
свободных (управляемых) переменных; ![]() — заданная матрица
— заданная матрица ![]() ,
, ![]() —
вектор,
—
вектор, ![]() — нижняя и верхняя границы измерения
— нижняя и верхняя границы измерения ![]() -ой компоненты вектора управляющих
воздействий. Известно множество функций цели
-ой компоненты вектора управляющих
воздействий. Известно множество функций цели ![]() ,
которые целесообразно максимизировать выбором
,
которые целесообразно максимизировать выбором ![]() .
Альтернатива
.
Альтернатива ![]() называется эффективной, если на
называется эффективной, если на ![]() не существует альтернативы
не существует альтернативы ![]() , для которой выполнялись бы неравенства
, для которой выполнялись бы неравенства ![]() и хотя бы одно из них было строгим.
Эффективную альтернативу называют оптимальной по Парето. Для любой эффективной
альтернативы
и хотя бы одно из них было строгим.
Эффективную альтернативу называют оптимальной по Парето. Для любой эффективной
альтернативы ![]() существует вектор весовых коэффициентов
существует вектор весовых коэффициентов ![]() с компонентами
с компонентами ![]() и
и ![]() такой, что критерий
такой, что критерий ![]() достигает на этой альтернативе
экстремального (максимального) значения. Последнее условие позволяет строить
области Парето как в пространстве критериев, так и в пространстве альтернатив.
Часто критерии приводят к безразмерному виду. Например, можно принять
достигает на этой альтернативе
экстремального (максимального) значения. Последнее условие позволяет строить
области Парето как в пространстве критериев, так и в пространстве альтернатив.
Часто критерии приводят к безразмерному виду. Например, можно принять 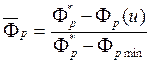 . Значение
. Значение ![]() можно
рассматривать как уровень достижимости (относительной) по критерию
можно
рассматривать как уровень достижимости (относительной) по критерию ![]() . Задача считается решенной, если
. Задача считается решенной, если ![]() является максимальной нижней границей для
всех
является максимальной нижней границей для
всех ![]() . Отсюда следует максиминная задача:
. Отсюда следует максиминная задача:
|
|
(2.2) |
решение которой следует из экстремальной задачи вида:
|
|
(2.3) |
В последнем случае можно вводить
приоритет 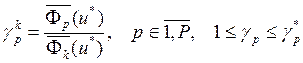 , где
, где ![]() —
оптимальное решение для
—
оптимальное решение для ![]()
![]() .
Число
.
Число ![]() (приоритет) показывает во сколько раз
относительная оценка
(приоритет) показывает во сколько раз
относительная оценка ![]() -го критерия важнее для ЛПР
относительных оценок
-го критерия важнее для ЛПР
относительных оценок ![]() -го критерия. Совокупность
значений
-го критерия. Совокупность
значений ![]() представляет собой вектор
представляет собой вектор ![]() -приоритетов, который позволяет построить
экстремальную задачу с приоритетом
-приоритетов, который позволяет построить
экстремальную задачу с приоритетом ![]() -го критерия. Затем надо
-го критерия. Затем надо
![]() в (2.3) заменить на
в (2.3) заменить на ![]() .
.
Весовые коэффициенты ![]() чаще
всего оценивают по формулам:
чаще
всего оценивают по формулам:
а) метод ранжирования:
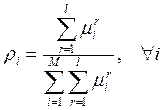 , где
, где ![]() — число
экспертов в группе;
— число
экспертов в группе; ![]() — ранг
— ранг ![]() -го
критерия у
-го
критерия у ![]() -го эксперта;
-го эксперта; ![]() — число
критериев.
— число
критериев.
б) метод приписывания баллов из ![]() :
:
![]() в а)
заменить на
в а)
заменить на 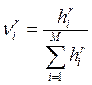 , где
, где ![]() — балл
— балл ![]() -го эксперта для
-го эксперта для ![]() -ой
функции цели.
-ой
функции цели.
в) частичное парное сравнение:
![]() в а)
заменить на
в а)
заменить на 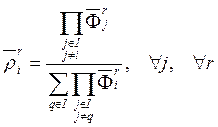 , где
, где ![]() —
относительная желаемая оценка
—
относительная желаемая оценка ![]() -го критерия
-го критерия ![]() -м экспертом, т.е.
-м экспертом, т.е. 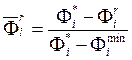 .
.
1. Уточнить вариант задания каждой группе студентов и представить задачу в виде (2.1);
2. Построить
модели задач по (2.2) без учета приоритетов и с приоритетами, задавая три
варианта ![]() из интервальной матрицы значений
приоритетов;
из интервальной матрицы значений
приоритетов;
3. Рассчитать
весовые коэффициенты ![]() по а) и б) и построить модели
задач в явном виде;
по а) и б) и построить модели
задач в явном виде;
4. Оценить абсолютные уступки (по всем критериям для задач без приоритетов и с приоритетами критериев), соответствующие равным относительным оптимальным уступкам;
5. Построить область Парето в пространствах критериев и переменных;
6. Оценить
весовые коэффициенты ![]() по в) и найти оптимальное
решение;
по в) и найти оптимальное
решение;
7. Представить результаты расчетов таблично и/или графически.
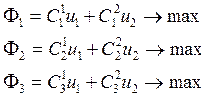
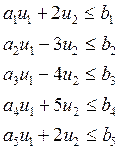
|
№ гр. |
|
|
|
|
|
|
вектор
|
вектор
|
|
1 |
-3 |
6 |
1 |
8 |
0,2 |
10 |
-6 3 -2 6 1 |
3 1 2 9 1 |
|
2 |
6 |
-1 |
0,3 |
4 |
10 |
0,8 |
4 -3 2 7 -8 |
9 7 5 4 2 |
|
3 |
2 |
3 |
1 |
0,15 |
1 |
1 |
9 -1 2 3 4 |
4 9 1 3 10 |
|
4 |
1 |
1 |
-10 |
1 |
3 |
10 |
-1 2 6 -5 8 |
6 2 1 5 4 |
|
5 |
4 |
-1 |
7 |
1 |
-4 |
-6 |
-10 -3 2 -7 4 |
9 1 4 10 6 |
|
6 |
3 |
6 |
9 |
2 |
4 |
7 |
3 2 6 -4 5 |
4 2 1 5 2 |
|
7 |
10 |
-2 |
6 |
-1 |
3 |
5 |
3 9 8 -1 4 |
4 8 6 3 5 |
|
8 |
8 |
-1 |
-9 |
-2 |
1 |
1 |
2 3 6 4 -8 |
8 1 10 2 6 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.