Метод наименьших квадратов. Методы оценивания вектора с использованием оценочного функционала. Архитектура диалоговой системы и ее функционирование

4.2.2. Метод наименьших квадратов

Предположим, что органу управления У известен конкретный вектор распределения априорных вероятностей на q и что, кроме этого, известна зависимость вектора  от . На основе заданных компонент вектора  и известной зависимостью  можно получить оценку  неопределенного параметра

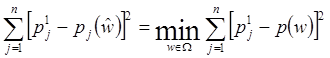 .                          (4.2)

Решение  этой задачи во многом определяется характером множества . При этом основные трудности ее решения связаны со случаем, когда  - замкнутое множество. В литературе, посвященной методу наименьших квадратов, традиционным является рассмотрение случая, когда , т.е. когда  совпадает с мерным евклидовым пространством. Это определение значительно упрощает решение задачи нахождения , поскольку позволяет использовать классический аппарат экстремума функций многих переменных без ограничений. В этом случае оценка находится из условий

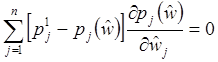  (1=1,…,q).                                      (4.3)

Рассматриваемая задача получения оценки  представляет собой упрощенный вариант применения метода наименьших квадратов.

4.2.3. Метод максимального правдоподобия

В этом методе определяется функция правдоподобия  в виде 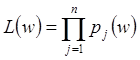 . Оценка второго рода , которую принято называть оценкой максимального правдоподобия неопределенного параметра , определяется из условия достижения максимума функции  при , т.е. из условия

                                                (4.4)

Оценка максимального правдоподобия  удовлетворяет следующей системе уравнений (при условии, что -открытое множество):

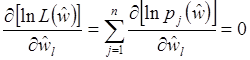                  (1=1,…,q)            (4.5)

4.2.4. Эвристический метод

Данный метод используется тогда, когда неизвестна плотность  распределения вероятностей параметра (1=1,…,q). Нахождение плотности  является самостоятельной задачей, решаемой органом управления У на основе статистических данных.

Построение плотностей  параметра  этим методом является упрощенным подходом и часто используется в моделях сетевого планирования. Сущность этого метода заключается в следующем. Орган управления по каждой компоненте (1=1,…,q) находит или задает следующие три оценки, характеризующие возможные значения параметра :

- моду , которая носит название наиболее вероятного значения параметра , при этом величина  устанавливается органом управления У на основе знаний (опыта) и является априорной оценкой;

- нижнюю грань  области  определения параметра ;

- верхнюю грань  области  определения параметра .

На основе этих трех задаваемых оценок определяется математическое ожидание  и дисперсия   параметра (1=1,…,q)  по формулам

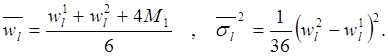      (4.6)

При расчете математического ожидания и дисперсии неизвестного параметра  по этим формулам особые трудности вызывает необходимость задания значения моды распределения, особенно в тех случаях, когда орган управления У не располагает достаточной статистикой. Поэтому в качестве приближенной плотности распределения параметра  в сетевом планировании предлагается использовать распределение (типа «b - распределения») вида

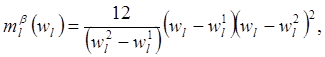                     (4.7)

вероятностные характеристики которого определяются следующим образом:

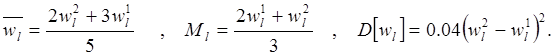 (4.8)

Распределение  характеризуется лишь двумя параметрами ,  и положительным эксцессом. В некоторых случаях эмпирическое распределение  может служить хорошей приближенной оценкой распределению .

В работах по сетевому планированию, помимо b - распределений, используется логарифмически нормальное распределение плотностью

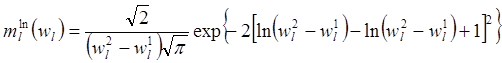              (4.9)

для которого  

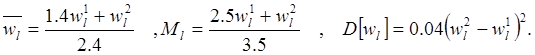    (4.10)

Эти распределения мало отличаются друг от друга, характеризуются двумя параметрами  и , и каждое из них может быть использовано в качестве приближенной оценки плотности  распределения вероятностей параметра. Отметим, что изложенная выше упрощенная методика оценки плотностей  распределения вероятностей параметра  на основе двух задаваемых оценок  и (1=1,…,q) отличается рядом преимуществ, гарантирующих использование небольшого объема знаний о контролируемых факторах неопределенных параметров . 

4.2.5. Вариационный метод

Сущность этого метода заключается в решении вариационной задачи выбора плотности   распределения вероятностей параметра  (1=1,…,q) по данным наблюдений 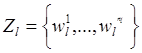 из условия (4.11)

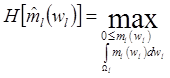                          (4.11)

при ограничениях

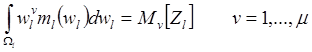             (4.12)

Здесь через  обозначена энтропия Шеннона неопределенного параметра, которая равна

                      (4.13) а  - точечная оценка -го момента распределения

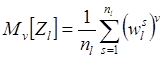                        (4.14)

На основе применения метода множителей Лагранжа для учета ограничений типа равенств в сформулированной вариационной задаче можно показать, что плотность  распределения параметра  имеет следующий вид:

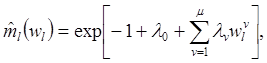                 (4.15)

причем множители Лагранжа  определяются из условий

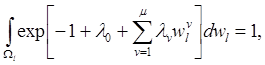             (4.16)     

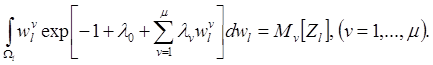                 (4.17)

Дальнейшее развитие вариационного метода нахождения плотности  распределения вероятностей параметра  по данным наблюдений 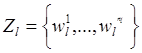 может быть продлено двумя способами. Первый способ состоит в замене энтропии Шеннона другими функциями неопределенности, например