Метод наименьших квадратов. Методы оценивания вектора с использованием оценочного функционала. Архитектура диалоговой системы и ее функционирование, страница 3

-   аддитивна по состояниям .

Формализм Джейнса постулирует: наименее сомнительным представлением вероятностей будет такое представление, которое максимизирует неопределенность при учете всей заданной информации.

Согласно Джейнсу, принцип максимальной неопределенности можно рассматривать как распространение принципа недостаточного основания Бернулли-Лапласа (суть: если данных к тому чтобы считать одно состояние среды из множества  более вероятным, чем любое другое состояние среды из множества , то априорные вероятности  состояний среды нужно считать равными) со следующим отличием: принятие распределения, обеспечивающего максимальную неопределенность, можно мотивировать тем позитивным соображением, что оно определяется однозначно как допускающее наибольшую вариабельность относительно недостающей информации вместо негативного соображения, что нет оснований предложить что-либо другое. С математической точки зрения распределение с максимальной неопределенностью обладает тем важным свойством, что в нем могут быть учтены все возможности.

Таким образом, применение принципа позволяет определить точечную оценку из условий (4.26)

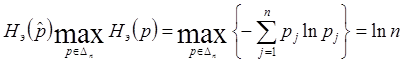                       (4.26)

в виде

Существенным преимуществом принципа Гиббса-Джейнса является возможность получения оценок априорного распределения, в которых органом управления У могут быть установлены ограничения на распределение априорных вероятностей состояния среды, например, в форме задания средних и дисперсионных характеристик значений оценочного функционала .

В качестве простейших возможны следующие два типа ограничений. Ограничения на байесово значение оценочного функционала вида , где в качестве  может быть выбрана, например, оценка среднего значения оценочного функционала для решения .

Ограничения первого типа на дисперсию значений оценочного функционала могут иметь вид , где в качестве  может быть выбрана, например, оценка дисперсии значения оценочного функционала для решения :

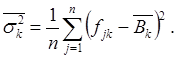                               (4.27)

Аналогичным образом могут выбираться ограничения на моменты более высокого порядка, как в форме равенств, так и в форме неравенств. Например, для ограничений второго типа можно рассматривать следующие неравенства:

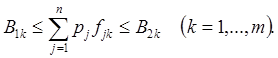                 (4.28)

В качестве способов задания  и  могу быть использованы границы доверительного интервала . Аналогичные неравенства могут быть введены и для учета дисперсионных значений оценочного функционала.

С математической точки зрения ограничения в виде равенств и неравенств при использовании принципа максимальной неопределенности приводят к решению задач выпуклого математического программирования. Для учета ограничений в форме равенств можно использовать аппарат теории множителей Лагранжа. Для учета ограничений в форме неравенств необходимо использовать специальные методы учета ограничений, например такие, как методы погружения, обобщенные методы множителей Лагранжа и т.д.

Существует обобщение принципа максимума Гиббса-Джейса, которое заключается в нахождении оценки  априорного распределения на  при использовании какой-либо функции неопределенности первого рода вместо энтропии Шеннона. К таким функциям относятся:

-  функция неопределенности де Грота

;

-  информационная энтропия вида

;

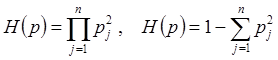-  структурная - энтропия

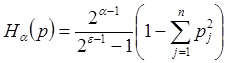 для ;

-  энтропия Реньи порядка

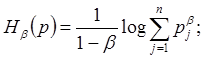
-  функция неопределенности порядка  типа

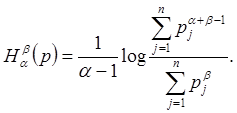
5. Архитектура диалоговой системы и ее функционирование

Под архитектурой любой системы понимают совокупность функциональных элементов, объединенных определенной композицией для достижения цели и/или постановки и решения прикладной задачи. В силу этого определения, связи в такой системе оказываются переменными и формируемыми для выполнения конкретной операции. Представлять архитектуру можно в различных разрезах, но с учетом прикладных аспектов, представляется важным плоскость информационно – алгоритмического характера и функциональная направленность разрабатываемой ДС.

Функционирование ДС

Под функцией подразумевают свойство объекта необходимое и достаточное для достижения цели. Отсюда ДС как сложная и обладающая динамикой система, должна быть наделена совокупностью функций, необходимых для реализации функций принятия решений. С таких позиций структуру ДС поясняет рис.5.1.

Представленная на рис.5.1. структура, с позиций коммуникативного общения ЛПР и средств ДС, выполняет следующие функции:

-  защищает формально – логическую часть ДС то разрушения;

-  распределяет запросы по разрушенным каналам обслуживания;

-  поддерживает активность диалога посредством обратной связи;

-  обслуживает запрос информационно и логически.

Структура функций ДС

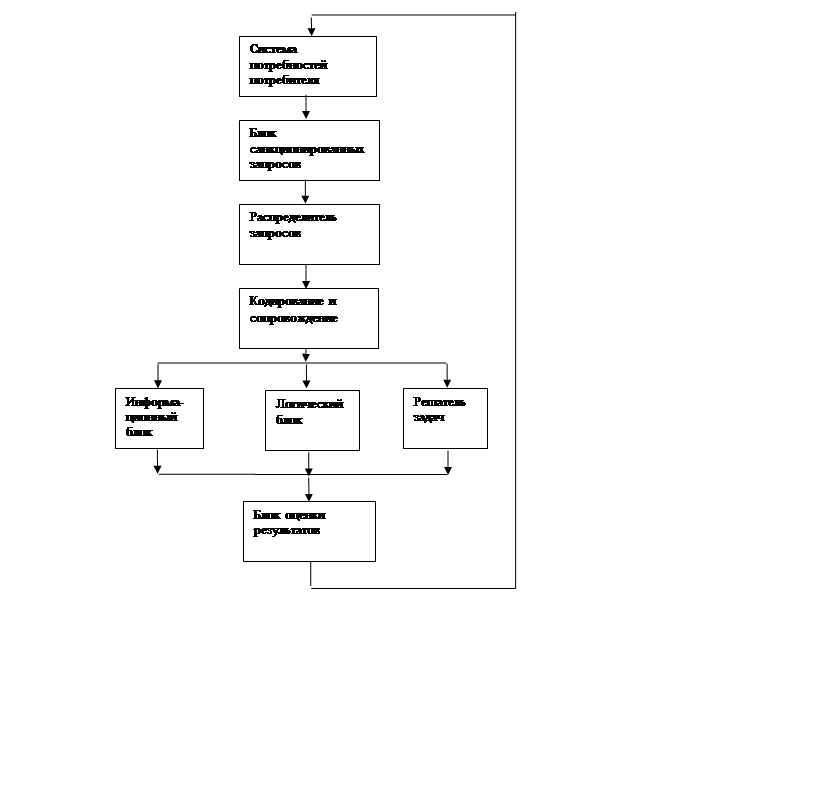
Рис.5.1

Совокупность перечисленных функций названа в работе [15] простой, в смысле реализации нижних границ рационального диалога. Таким образом, разрабатываемую ДС можно отнести к классу простых.