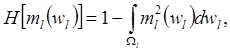Математика \ Теория вероятностей и математическая статистика

Метод наименьших квадратов. Методы оценивания вектора с использованием оценочного функционала. Архитектура диалоговой системы и ее функционирование, страница 2

(4.18)

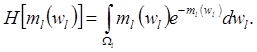(4.19)

Второй способ состоит в замене вариационной задачи максимизации при ограничениях в форме равенств (получающихся при использовании лишь точечных оценок на первые моментов) вариационной задачей с ограничениями в форме неравенств вида (4.20)

. (4.20)

Где , - границы доверительного интервала для значений n - го момента распределения .

4.3. Методы оценивания вектора с использованием оценочного функционала

4.3.1. Методы третьего рода

Полученные в предыдущих разделах оценки неопределенного параметра не были связаны с оценочным функционалом. Учитывая это, изложим некоторые подходы к получению оценок третьего рода с учетом фактора влияния их на значение оценочного функционала.

Если органу управления У требуется оценить неопределенный параметр , то свою оценку он может основывать на обработанных тем или иным способом результатах статистических наблюдений. Выбранная органом управления оценка параметра зависит от свойств наблюдаемых совокупностей и, следовательно, представляет собой случайную величину.

Для наглядности представления об оценках третьего рода рассмотрим случай . Предположим, что является истинным значением неопределенного параметра, которое неизвестно органу управления, а - оценка этого параметра. Определим параметрическое сожаление как функцию вида (4.21)

(4.21)

удовлетворяющую условиям >0, =0 при , причем увеличивается с ростом разности между и .

В качестве функции с указанными выше свойствами разумно выбрать следующие зависимости:

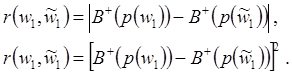(4.22(а,б))

Параметрическое сожаление может иметь вид, показанный на рис.4.2.

Статистическую совокупность 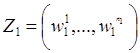называют выборкой. Определим стратегию выбора оценки органом управления У как некоторый алгоритм для получения оценки в соответствии с каждой возможной выборкой 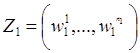, которую будем называть стратегией оценки и обозначать .

Параметрическое сожаление

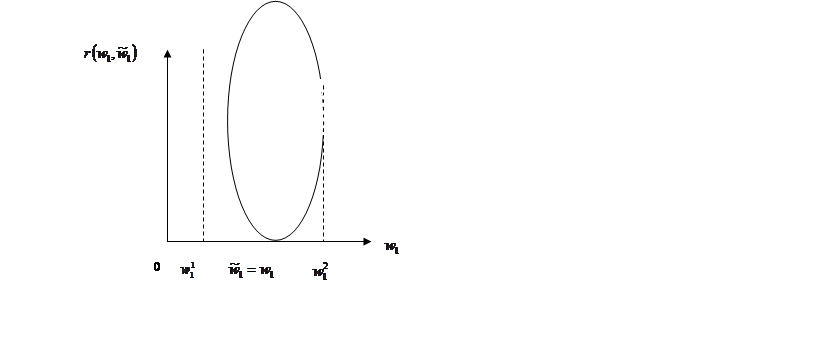
Рис.4.2

Таким образом, стратегия оценки есть случайная функция, ставящая в соответствие каждому элементу с компонентами из параметрического множества элемент , поэтому оценку как функцию обозначим через =. В качестве простых стратегий оценок могут быть выбраны среднее значение, медиана, мода, квантили и другие параметрические характеристики случайной величины.

Определим параметрическую функцию риска для стратегии , приводящей к оценке , в виде (4.23)

Тогда задача оптимального параметра формулируется следующим образом: требуется найти стратегию оценки , дающую оптимальную оценку, удовлетворяющую условию

В прикладных задачах исследования оценок третьего рода вместо выражения для параметрического сожаления пользуются приближенными равенствами вида

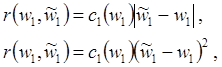(4.24)

которые являются достаточно приемлемой аппроксимацией при значениях в окрестности истинного значения параметра .

Получения стратегий оценок могут быть использованы различные методы: методы моментов, максимального правдоподобия, байесовых оценок и др. Использование двух последних методов связано с требованием наличия определенной информации о законах распределения неопределенного параметра и условных законах распределения.

При рассмотрении выборок больших объемов стратегию оценки можно представить как последовательность частных стратегий оценок, каждую из которых можно построить применительно к выборке определенного объема, и исследовать поведение этой последовательности при .

Такой подход может быть использован для упрощения математических преобразований, т.к. предельное поведение последовательности стратегий оценок проще исследовать. Кроме того, такой подход позволяет устранить некоторые критерии разумности стратегий оценок при заданных объемах выборки.

4.3.2. Принцип максимальной неопределенности Гиббса-Джейнса

Согласно принципу максимума Гиббса-Джейнса наиболее характерными распределениями вероятностей состояний неопределенной среды являются такие распределения, которые максимизируют выбранную меру неопределенности при заданной информации о «поведении» состояний среды. Впервые такой подход использовал Гиббс для нахождения экстремальных функций распределения физических ансамблей частиц. Впоследствии Джейнсом был предложен формализм восстановления неизвестных законов распределения случайных величин при наличии ограничений из условий максимума энтропии Шеннона вида (4.25)

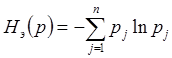. (4.25)