Расчет вероятности выбора белого шара из трех урн

Пример. Имеем три урны с содержимым на рис.

Субъект подходит к ним и выбирает наугад одну урну и вынимает из нее наугад шар. Какова вероятность того, что шар окажется белым?

Имеем событие A

A={появление белого шара}

Относительно формы проведения опыта можно выдвинуть три гипотезы:

H₁={выбор субъектом первой урны};

H₂={ выбор субъектом второй урны };

H₃={ выбор субъектом третей урны }.

Относительно события гипотезы на нашем Ω образуют полную группу, т.к. больше выбирать нечего!

Можем сразу оценить P(H₁)= P(H₂)= P(H₃)=1/3

Найдем условные вероятности вида P(A|H_i), i=1,3 – это легко сделать частотными методами. Имеем:

P(A|H₁)=2/5;  P(A|H₂)=4/6;  P(A|H₃)=1

Вероятность P(A) определим по формуле полной вероятности, т.е.

P(A)=1/3(2/5+4/6+1)=11/15

Более насущный пример применения формулы полной вероятности.

Имеется N экзаменационных билетов, причем среди них n «счастливых».

Студенты подходят за билетами один за другим. У кого больше шансов взять «счастливый» билет: у того, кто подошел первым или у того, кто подошел вторым?

Ясно, что мы должны сравнить вероятности взятия наугад «счастливого» билета для указанных субъектов.

Вероятность взять «счастливый» билет для первого студента P₁(“C”)=n/N, т.к. это случай шансов.

Относительно второго студента можно сформулировать две гипотезы:

H₁={Первый студент взял «счастливый» билет};

H₂={Первый студент взял «плохой» билет}.

Тогда для оценивания вероятности P₂(“C”) – второй взял «счастливый» билет по формуле полной вероятности имеем:

P₂(“C”)=P(H₁)P₁(“C”|H₁)+P(H₂)P₂(“C”|H₂)=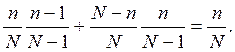

Итак, шансы для наших студентов взять наугад «счастливый» билет при последовательных действиях оказались равными.