Элементарные события. Таблица соответствий теории множеств и теории вероятности

называют  элементарными  событиями.   Само   множество   Ω   называют   пространством элементарных событий с элементами  (ПЭС).

Полезен такой опыт: дважды бросаем правильную монетку и нас интересует вероятность появления, скажем, двоек вида «герб-герб». В таком случае нас интересуют пары вида «ГГ», «РГ» и т.д.

В таком случае ПЭС формируется в явном виде. Состав его следующий: Ω = { ГГ, ГР, РГ, РР }, где «Г» на первом месте означает появление герба при первом бросании (или на первой монете), а «Р» - появление решки.

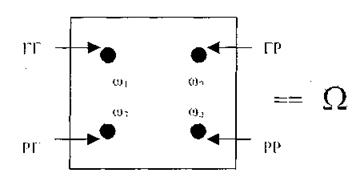
Сейчас мы можем с каждым событием связать точку из ПЭС или множество точек, т.е. подмножество из Ω, оставляя обозначение как и для событий. Например, зная Ω, мы можем в нем выделить его часть тех и только тех точек, которые влекут появление, например, событий А. Обозначим такое подмножество Ω_A. Тогда остальная часть множества Ω не благоприятствует появлению события А, т.е. есть событие, которое отличается от события А.

Такое событие называют противоположным к событию А и обозначают. Множество Ω (ПЭС) можно разбить на части следующим образом. Вели в результате опыта произошло, то событие А реализовалось, в противном случае - реализовалось событие .

Таким образом, подмножество А с Ω интерпретирует событие А, т.е. для нас реализация события А есть некоторое подмножество Ω, включающее те и только те точки, которые благоприятствуют событию A. Пусть для нашего Ω событие А = {выпадение герба на первом месте}. Тогда Ω _A = (ГГ, ГР) и n_A = | Ω _A| = 2, а n = | Ω | = 4. При наших допущениях:  Р(А) =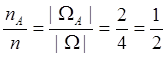, что соответствует нашей интуиции. Ясно, что из нашего подхода P(Ω) = 1, аР(0) = 0.

Представление ПЭС как конечного или счетного множества удобно в том плане, что есть возможность использовать элементарные алгебры множеств. В теории вероятностей есть своя специфика и она отражена в следующей таблице.

Таблица соответствий ТМ и ТВ.