n p
Рис.3.1
В таблице обозначено: n – размерность квадратной матрицы A. В примере три уравнения состояния, поэтому n=3. Следовательно, матрицаA квадратная и состоит из трех строк и трех столбцов:
.
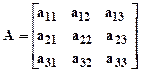(3.12)
Матрица В состоит из n=3строк и p=2 столбцов. Количество столбцов p равно числу входных воздействий. В примере два воздействия: U1=uy и U2=ic. Размерность матрицы С q xn, где q-число выходов. В примере три выхода. Выходами являются напряжение якоря Uя, ток Iя и скорость w. Размерность D определяется количеством выходовq и количеством входов p.
Поскольку в нашем примере число входов p=2 и выходов q=3 матрицы B и С примут вид, причем C диагональная матрица:
,
, 
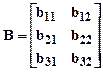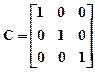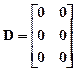. (3.13)
Применение изложенных правил продемонстрируем на примере.
Пример 1. Построить модель объекта в уравнениях состояния, если дано: Тп=0.01, Tя=0.04 с, Rя=0.5 Ом, Тм=0.1 с, Uян=220 В, wн=105, Iн=21А, kп=22.
Перейдем к работе в системе Matlab-Control System Toolbox. Запустить Matlab можно из меню “Пуск” или с помощью ярлычка на рабочем столе. Окно Matlab для ввода команд пакета Control System Toolbox и других пакетов расширения, имеет вид, приведенный на рис.3.2.
 |
Рис. 3.2.
При создании модели состояния в Matlab - Control System Toolbox необходимо предварительно с помощью Matlab ввести промежуточные константы cf и k, используя данные из задания:
cf=сф= (Uян
– RяIн)/wн, Ik=Uян/Rя,
k=Ik/Iн=Uян/(RяIн),
а затем ввести численные значения элементов матриц используя формулы, следующие за (3.9):
a22=
, a31=
b22=b22=0,
.
По формуле Matlab
A = [a11 a12 a13; a21 a22 a23; a31 a32 a33], (3.14)
ввести матрицу A, где первые три цифры – элементы первой строки, вторые – второй, третьи – третей. Элементы строк разделяются точкой с запятой.При трех выходах w, iЯ, uЯ и двух входных воздействиях uy и ic матрица B состоитиз трех строк и двух столбцов и вводится следующим образом:
B = [b11 b12; b21 b22; b31 b32]. (3.15)
С=[1 0 0; 0 1 0; 0 0 1]; D=[0 0; 0 0; 0 0].
Для ввода непрерывной модели в уравнениях состояния необходимо воспользоваться функцией Matlab
Sss=ss(A,B,C,D), (3.16)
а преобразование аналоговой модели в цифровую модель в уравнениях состояния осуществить с помощью другой функции Matlab
Zss=c2d(Sss, T, ’metod’), (3.17) где Sss, Zss – соответственно имена непрерывной и цифровой моделей в уравнениях состояния, T – период дискретизации, metod – метод дискретизации, это слово следует заменить одним из следующих значений, сохраняя кавычки:
‘zoh’ – экстраполятор нулевого порядка, принят по умолчанию и поэтому может при вызове функции не указываться.
‘foh’ – экстраполятор первого порядка.
‘tustin’ – подстановка Тастина.
Период дискретизации T следует выбирать из условия T£0.5Tmin, где Tmin наименьшая постоянная времени системы. Оценку правильности выбора T можно выполнить несколькими прогонами системы, каждый раз уменьшая T в два раза. Последний и предпоследний прогоны следует выводить в одно окно. В этом случае кривые процессов будут выводиться наложенными друг на друга, что существенно облегчит сравнение. Если в последних двух прогонах переходные процессы совпадают, то следует выбрать T из предпоследнего прогона. Необходимо также, чтобы амплитуда первого скачка выходного напряжения усилителя мощности была не больше 30%. Это даст гарантию, что не будет превышено предельно допустимое значение темпа нарастания тока якоря. Допустимый темп нарастания тока определяется по паспортным данным двигателя и находится в пределах 10…50 номинальных токов за секунду.
Более тонкую оценку можно выполнить по весовым функциям.
Переопределить шаг дискретизации функции Zss можно с помощью функции
Zss1=d2d(Zss,T),
где Zss – исходная цифровая модель,
Zss1 – модель с измененным шагом дискретизации.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.