где Uя - напряжение на якоре двигателя;
Uу, kп, Тп – соответственно напряжение на входе, коэффициент преобразования и постоянная времени управляемого источника энергии.
Электрические процессы в якорной цепи двигателя моделируются дифференциальным уравнением равновесия напряжений:
Uя(t)-E(t)=RяIя(t)+LяdIя/dt, (2.2)
где E - противо-ЭДС обмоток якоря;
Iя - ток якорной цепи;
Rя - активное сопротивление якорной цепи;
Lя - индуктивность якорной цепи.
Механическая составляющая электромеханической системы описывается уравнением движения
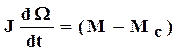 , (2.3) где M=cфIя,
(2.4)
, (2.3) где M=cфIя,
(2.4)
J - момент инерции электромеханической системы с учетом объекта управления;
W - скорость вращения вала двигателя;
с – конструктивная постоянная двигателя;
Ф – магнитный поток двигателя;
Mc – момент нагрузки двигателя; причем скорость w и ЭДС двигателя связаны соотношением:
E=cф![]() .
(2.5)
.
(2.5)
Соотношения (2.1)…(2.5) представляют собой непрерывную математическую модель электромеханической системы, причем дифференциальные уравнения (2.1), (2.2) и (2.3) отображают динамические процессы, а алгебраические уравнения (2.4) и (2.5) – статические связи между переменными электромеханической системы.
Разрешив уравнения (2.1), (2.2) и (2.3) соответственно относительно производных скорости, тока и напряжения на якоре двигателя, с учетом соотношений (2.4) и (2.5), получим систему непрерывных уравнений, представляющих собой модель электромеханической системы в нормальной форме Коши:
![]() , (3.1)
, (3.1)
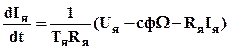 , (3.2)
, (3.2)
![]() , (3.3)
, (3.3)
где Тя=Lя/Rя - постоянная времени якорной цепи двигателя.
С целью масштабирования и обобщения результатов исследований для систем с различными числовыми характеристиками введем относительные значения переменных:
![]() .
.
где ![]() ,
, ![]() ,
, ![]() -
соответственно номинальное напряжение на якоре двигателя, номинальный ток и
номинальная скорость двигателя. Используя введенные соотношения уравнения
(3.1), (3.2) и (3.3) перепишем в относительных единицах:
-
соответственно номинальное напряжение на якоре двигателя, номинальный ток и
номинальная скорость двигателя. Используя введенные соотношения уравнения
(3.1), (3.2) и (3.3) перепишем в относительных единицах:
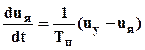 ,
,
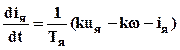 ,
,
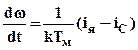 , где Tм
=
, где Tм
= 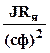 ,
, ![]() –
соответственно электромеханическая постоянная времени и коэффициент отношения
тока короткого замыкания к номинальному току двигателя.
–
соответственно электромеханическая постоянная времени и коэффициент отношения
тока короткого замыкания к номинальному току двигателя.
Правые части последних уравнений дополним недостающими переменными, входящими в левые части системы уравнений. Причем переменные введем в том порядке, в котором они появляются в левых частях уравнений. Чтобы сохранить справедливость уравнений добавленные переменные умножим на нулевые коэффициенты:
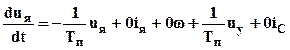 (3.4)
(3.4)
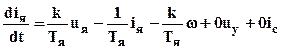 , (3.5)
, (3.5)
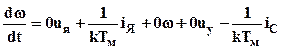 .
(3.6)
.
(3.6)
Перепишем систему уравнений (3.4), (3.5) и (3.6) в обобщенной форме, используя замену переменных uя=x1, iя=x2, w=x3 и вводя новые обозначения для коэффициентов:
![]() (3.7)
(3.7)
![]() , (3.8)
, (3.8)
![]() , (3.9)
, (3.9)
где ![]() ,
,
![]()
![]() ,
,
![]() .
.
Система уравнений (3.7), (3.8) и (3.9) называется уравнениями состояния, а cовокупность переменных x1 x2 x3 – переменными состояния. Кроме того, уравнения состояния дополняются уравнениями выхода, связывающие переменные состояния с физическими координатами системы:
y1=uя, y2=iя , y3=w. (3.10)
Чтобы, используя среду Matlab, создать модель объекта в пространстве состояния, необходимо привести уравнения состояния (3.7), (3.8) и (3.9) и выхода (3.10) к стандартному векторно-матричному виду:
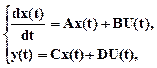 (3.11)
(3.11)
где 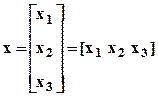 T - вектор состояния,
T - вектор состояния,
y - вектор выхода,
U = [U1 U2]=[uy ic] - вектор входных воздействий,
A и C – соответственно матрицы коэффициентов при переменных состояния x уравнений состояния и уравнений выхода,
B и D – соответственно матрицы коэффициентов при входных воздействиях U уравнений состояния и уравнений выхода.
Вид матриц A, B, C и D зависит от числа переменных состояния n, входов p и выходов q. Для определения размерностей матриц и векторов удобно воспользоваться таблицей на рис.3.1.
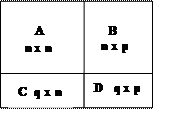
n
q
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.