Метрология и технические измерения отрасли: Программа, методические указания и контрольные задания, страница 7

Примечание. Погрешностью вторичного прибора пренебречь.

4.2.  Определение погрешности косвенных измерений

Косвенныминазывают измерения, при которых искомое значение величины находят на основании известной зависимости между этой величиной и величинами, определяемыми прямым измерениям. При косвенных измерениях путем прямых измерений находят значения величин-аргументов, а значение измеряемой величины А определяют путем вычисления по формуле:

                           (16)

где a₁ , a₂, ..., a_N – величины-аргументы.

Функция f должна быть определена теоретически или установлена экспериментально с погрешностью, которой можно пренебречь.

Метод обработки результата зависит от вида измерений: однократные или многократные, с линейной зависимостью между аргументами или нелинейной, а также наличия корреляции между результатами прямых измерений.

Примером косвенных измерений могут служить измерения плотности однородного тела по его массе и объему; электрического сопротивления по падению напряжения и силе тока; энергии, переданной теплоносителем и т. д.

Обработка результатов косвенных измерений производится в соответствии с /3/. Как и при прямых измерениях отдельно оцениваются случайные и неисключенные систематические погрешности, а результирующая погрешность определяется на основе композиции распределений случайных и неисключенных систематических погрешностей.

Если искомое значение A связано с m измеряемыми аргументами a₁, a₂, … , a_m  уравнением:

A = b₁a₁ + b₂ · a₂, + ...+ b_m · a_m ,                       (17)

где b₁, b₂,..., b_m - постоянные коэффициенты при аргументах a₁, a₂ … , a_m соответственно;

а погрешности прямых измерений не коррелированны  (что бывает чаще всего), то среднее квадратическое отклонение результата косвенного измерения  S(Ã)  (СКО среднего) вычисляют по формуле:

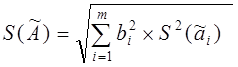                                          (18)

где  – среднее квадратическое отклонение результата измерения аргумента a_i

Доверительные границы случайной погрешности результата косвенного измерения при условии, что распределения погрешностей результатов измерений аргументов не противоречат нормальным распределениям, вычисляют (без учета знака) по формуле:

                                        (19)

Если случайной погрешностью можно пренебречь, то доверительные границы неисключенной систематической погрешности результата косвенного измерения  (без учета знака) при вероятности P вычисляют по формуле:

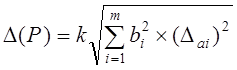                               (20)

где k – поправочный коэффициент, определяемый принятой доверительной вероятностью и числом m.

При доверительной вероятности Р = 0,95 поправочный коэффициент k принимают равным 1,1. При доверительной вероятности Р = 0,99 и  числе суммируемых составляющих m>4 поправочный коэффициент принимают равным 1,4. Если же число составляющих m≤4, то поправочный коэффициент k≤1,4. Более точное значение k определяется по /3/.

Если функция (16) нелинейна, то границы неисключенной систематической погрешности результата косвенного измерения вычисляют по формуле:

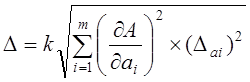,                          (21)

В некоторых случаях зависимость (16) представляется в виде таблиц, тогда формулу (21) можно записать в виде:

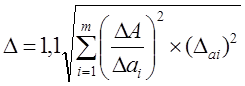 ,                          (22)

где ΔA=A₂ – A₁ – разность значений косвенного измерения, соответствующая разности прямых измерений i-го аргумента: Δа_i=a_i2 – a_i1

Если функция (16) может быть представлена в виде: 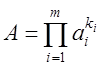, то используют формулу для оценки относительных погрешностей:

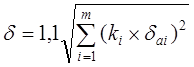                                     (23)

где  – относительная погрешность измерения i-го аргумента.

Если неисключенная систематическая и случайная погрешности таковы, что выполняется неравенство:, то доверительную границу погрешности результата косвенного измерения ∆(P) вычисляют по формуле

                                        (24)

где K – коэффициент, зависящий от доверительной вероятности и от отношения .

Таблица 2. Значения коэффициента K для вероятности P = 0,95