Метрология и технические измерения отрасли: Программа, методические указания и контрольные задания, страница 5

Оценку суммарного среднего квадратического отклонения результата измерения вычисляют по формуле

                                    (14)

Коэффициент K вычисляют по эмпирической формуле:

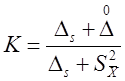                                            (15)

Пример. В результате измерений температуры были получены двадцать значений: (20,81; 21,19; 21,26; 21,10; 21,27; 21,19; 21,05; 21,07; 21,08; 21,13; 20,90; 20,82; 20,80; 20,98; 21,12; 21,02; 20,93; 21,20; 20,88; 20,82)⁰С. Измерения проводились термометром с погрешностью ±0,1 ⁰С

Для этой выборки среднее значение и СКО, определенные по формулам (3) и (4) составили соответственно: =21,031⁰С и S = 0,156⁰С

Больше всего от среднего значения отличается пятый результат (21,27⁰С). Проверим гипотезу о наличии грубой погрешности с помощью критерия Романовского. Для этого вычисляем среднее значение и СКО без подозрительного результата, которые составили соответственно: 21,018⁰С и 0,149⁰С. Значение критерия Стьюдента при заданной доверительной вероятности 0,95 и количестве наблюдений 19 равно 2,101 (таблица П1).

Тогда:

; =2,101∙0,149=0,313;          0,252<0,313, то есть данный результат не является грубой погрешностью и не отбрасывается.

Для проверки нормальности распределения используем составной критерий.

Определяем :

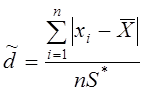= 0,87,

                                 

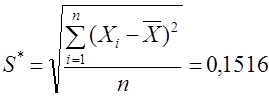
Зададимся уровнем значимости критерия q₁=0,1, тогда:

=0,7292,               =0,8788

т.е. 0,7292<0,87≤0,8788, следовательно, критерий 1 выполняется.

Критерий 2.

Зададим q₂=5%, тогда значение Р, соответствующее n=20 и q₂=5%, равно 0,98, а z_P/2=2,33 (см табл.3).

Следовательно:

z_P/2 σ=2,33∙0,156=0,3645

В соответствии с табл. 3 m=1, т.е. допустимо, чтобы не более одного значения  превысило 0,3645. В данном случае максимальная разница составляет 0,252, т.е. распределение по 2 критерию также можно считать нормальным.

Определим доверительные границы погрешности результата измерения, для чего проверим соотношения случайной и неисключенной систематической погрешностей:

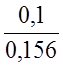==0,64<0,8.

Следовательно, неисключенной систематической погрешностью можно пренебречь, а погрешность результата измерений представить в виде: D =.

Ответ: Т=±∙t_p=21,031± 2,094∙0,156=21,03±0,33 ⁰С (n=20, Р_Д=0,95)

Задачи. Исходные данные для вариантов 1-19 приведены в табл.1

Таблица 1.Условия задач для задания 1